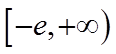(I)求出
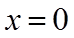
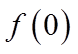
(II)令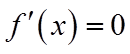

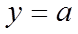
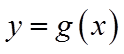
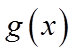
(III)令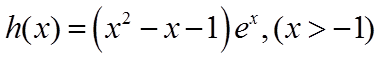

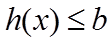
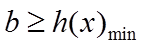
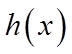
【详解】(I)
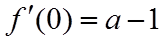
又
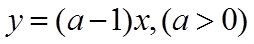
(II)令
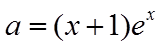
令
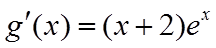
当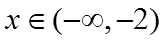
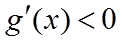

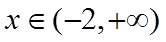
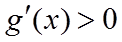
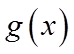
当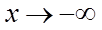
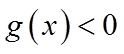

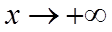
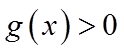
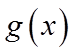
所以当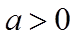
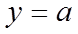

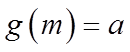
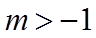
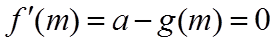
当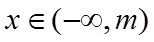

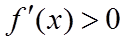
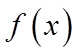
当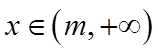

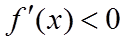
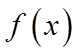

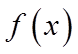
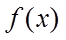
(III)由(II)知
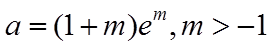
所以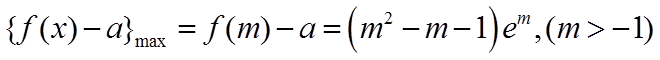
令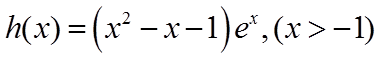
若存在a,使得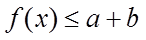

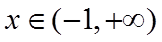
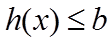
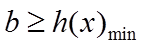

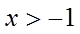
当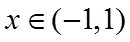
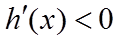

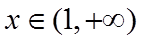
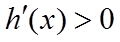
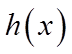
所以
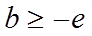
所以实数b的取值范围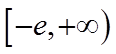
(I)求出
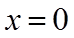
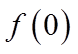
(II)令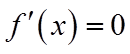

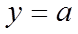
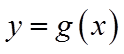
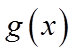
(III)令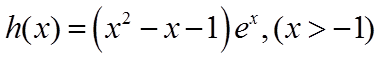

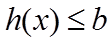
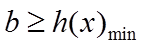
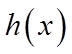
【详解】(I)
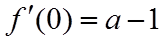
又
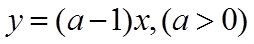
(II)令
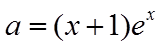
令
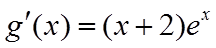
当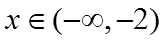
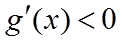

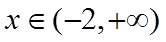
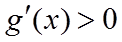
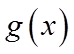
当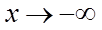
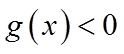

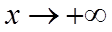
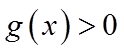
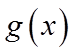
所以当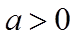
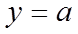

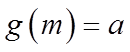
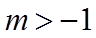
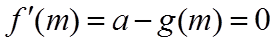
当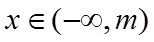

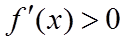
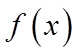
当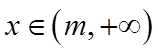

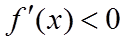
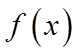

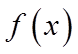
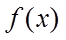
(III)由(II)知
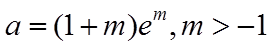
所以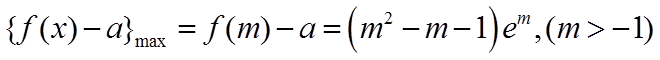
令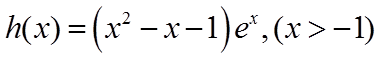
若存在a,使得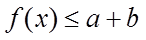

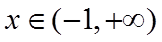
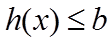
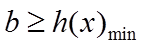

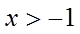
当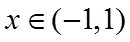
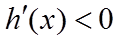

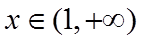
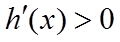
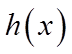
所以
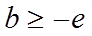
所以实数b的取值范围