(1)根据圆的几何性质可得出关于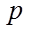
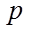
(2)设点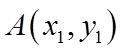
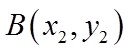
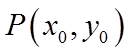
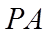
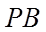
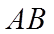
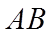
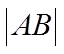
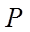
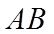
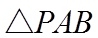
【详解】(1)抛物线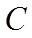
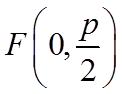
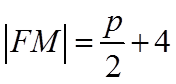
所以,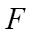
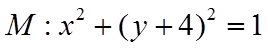
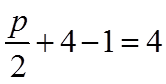
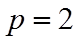
(2)抛物线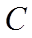
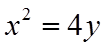
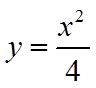
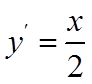
设点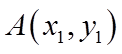
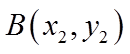
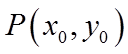
直线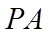
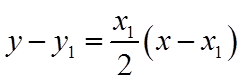
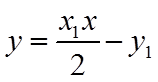
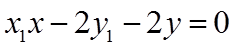
同理可知,直线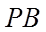
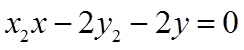
由于点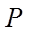
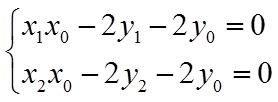
所以,点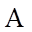
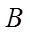
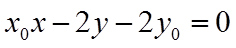
所以,直线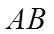
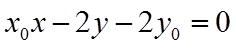
联立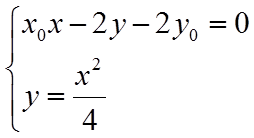
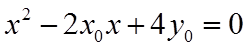
由韦达定理可得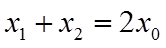
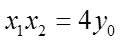
所以,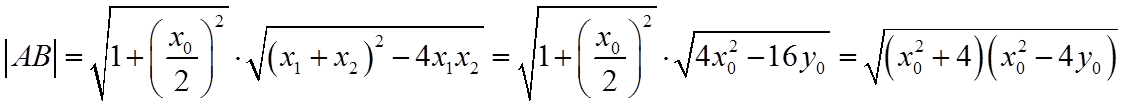
点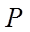

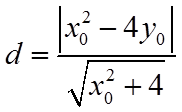
所以,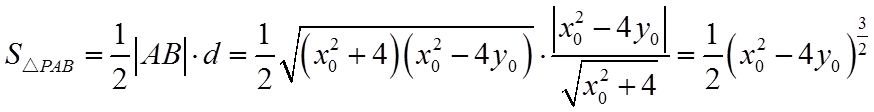
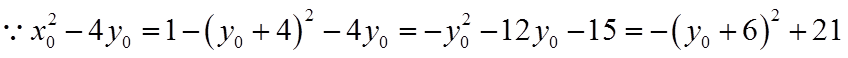
由已知可得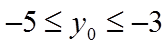
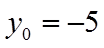
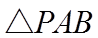
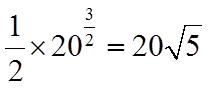
【点睛】方法点睛:圆锥曲线中的最值问题解决方法一般分两种:
一是几何法,特别是用圆锥曲线的定义和平面几何的有关结论来求最值;
二是代数法,常将圆锥曲线的最值问题转化为二次函数或三角函数的最值问题,然后利用基本不等式、函数的单调性或三角函数的有界性等求最值.