【考纲内容】

(一）通信基础

信道、信号、带宽、码元、波特、速率、信源与信宿等基本概念

奈奎斯特定理与香农定理;编码与调制

电路交换、报文交换与分组交换;数据报与虚电路

(二）传输介质

双绞线、同轴电缆、光纤与无线传输介质;物理层接口的特性

(三）物理层设备

中继器;集线器

【复习提示】

物理层考虑的是怎样才能在连接各台计算机的传输媒体上传输数据比特流，而不是指具体的传输媒体。本章概念较多，易出选择题，且涉及一些通信原理，读者不太明白的地方可以参考一些相关书籍，通信部分的内容也并非考研重点。复习时应抓住重点，如奈奎斯特定理和香农定理的应用、编码与调制技术、数据交换方式，以及电路交换、报文交换与分组交换技术等。

通信的目的是传送信息，如文字、图像和视频等。数据是指传送信息的实体。信号则是数据的电气或电磁表现，是数据在传输过程中的存在形式。数据和信号都可用“模拟的”或“数字的”来修饰:①连续变化的数据（或信号）称为模拟数据（或$\color{green}{\text{模拟信号}}$);②取值仅允许为有限的几个离散数值的数据（或信号）称为数字数据（或$\color{green}{\text{数字信号}}$)。数据传输方式可分为串行传输和并行传输。串行传输是指1比特1比特地按照时间顺序传输(远距离通信通常采用串行传输)，并行传输是指若干比特通过多条通信信道同时传输。

码元是指用一个固定时长的信号波形（数字脉冲）表示一位k进制数字，代表不同$\color{green}{\text{离散数值}}$的基本波形，是数字通信中数字信号的计量单位，这个时长内的信号称为k进制码元，而该时长称为码元宽度。1码元可以携带若干比特的信息量。例如，在使用二进制编码时，只有两种不同的码元:一种代表О状态，另一种代表1状态。

数据通信是指数字计算机或其他数字终端之间的通信。一个数据通信系统主要划分为信源、信道和信宿三部分。信源是产生和发送数据的源头。信宿是接收数据的终点，它们通常都是计算机或其他数字终端装置。发送端信源发出的信息需要通过变换器转换成适合于在信道上传输的信号，而通过信道传输到接收端的信号先由反变换器转换成原始信息，再发送给信宿。

信道与电路并不等同，信道是信号的传输媒介。一个信道可视为一条线路的逻辑部件，一般用来表示向某个方向传送信息的介质，因此一条通信线路往往包含一条发送信道和一条接收信道。噪声源是信道上的噪声（即对信号的干扰）及分散在通信系统其他各处的噪声的集中表示。

图2.1所示为一个单向通信系统的模型。实际的通信系统大多为双向的，即往往包含一条发送信道和一条接收信道，信道可以进行双向通信。

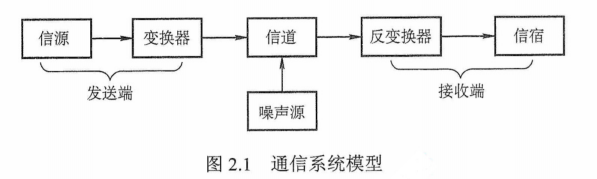
信道按传输信号形式的不同，可分为传送模拟信号的模拟信道和传送数字信号的数字信道两大类;信道按传输介质的不同可分为无线信道和有线信道。

信道上传送的信号有$\color{green}{\text{基带信号}}$和$\color{green}{\text{宽带信号}}$之分。基带信号将数字信号1和0直接用两种不同的电压表示，然后送到数字信道上传输（称为基带传输);宽带信号将基带信号进行调制后形成频分复用模拟信号，然后送到模拟信道上传输（称为宽带传输)。

从通信双方信息的交互方式看，可分为三种基本方式:

1)单向通信。只有一个方向的通信而没有反方向的交互，仅需要一条信道。例如，无线电广播、电视广播就属于这种类型。

2）半双工通信。通信的双方都可以发送或接收信息，但任何一方都不能同时发送和接收信息，此时需要两条信道。

3）全双工通信。通信双方可以同时发送和接收信息，也需要两条信道。

信道的极限容量是指信道的最高码元传输速率或信道的极限信息传输速率。

速率也称数据率，指的是数据传输速率，表示单位时间内传输的数据量。可以用码元传输速率和信息传输速率表示。

1）码元传输速率。又称波特率，它表示单位时间内数字通信系统所传输的码元个数（也可称为脉冲个数或信号变化的次数)，单位是波特（$\color{green}{\text{Baud}}$)。1波特表示数字通信系统每秒传输一个码元。码元可以是多进制的，也可以是二进制的，码元速率与进制数无关。

2）信息传输速率。又称信息速率、比特率等，它表示单位时间内数字通信系统传输的二进制码元个数（即比特数)，单位是比特/秒(b/s)。

注意:波特和比特是两个不同的概念，码元传输速率也称调制速率、波形速率或符号速率。但码元传输速率与信息传输速率在数量上却又有一定的关系。若一个码元携带n比特的信息量，则M波特率的码元传输速率所对应的信息传输速率为Mn比特/秒。

带宽原指信号具有的频带宽度，单位是赫兹（Hz)。在实际网络中，由于数据率是信道最重要的指标之一，而带宽与数据率存在数值上的互换关系，因此常用来表示网络的通信线路所能传输数据的能力。因此,带宽表示单位时间内从网络中的某一点到另一点所能通过的“最高数据率”。显然，此时带宽的单位不再是Hz，而是b/s。

具体的信道所能通过的频率范围总是有限的。信号中的许多高频分量往往不能通过信道，否则在传输中会衰减，导致接收端收到的信号波形失去码元之间的清晰界限，这种现象称为码间串扰。奈奎斯特（Nyquist）定理又称奈氏准则，它规定:在理想低通（没有噪声、带宽有限)的信道中，为了避免码间串扰，极限码元传输速率为 $\color{green}{\text{2W波特}}$ ，其中W是理想低通信道的带宽。若用V表示每个码元离散电平的数目（码元的离散电平数目是指有多少种不同的码元，比如有16种不同的码元，则需要4个二进制位，因此数据传输速率是码元传输速率的4倍)，则极限数据率为

理想低通信道下的极限数据传输速率=$2W log_2V$(单位为 b/s)

对于奈氏准则，可以得出以下结论:

1）在任何信道中，码元传输速率是有上限的。若传输速率超过此上限，就会出现严重的码间串扰问题，使得接收端不可能完全正确识别码元。

2）信道的频带越宽（即通过的信号高频分量越多)，就可用更高的速率进行码元的有效传输。

3）奈氏准则给出了码元传输速率的限制，但并未对信息传输速率给出限制，即未对一个码元可以对应多少个二进制位给出限制。

由于码元传输速率受奈氏准则的制约，所以要提高数据传输速率，就必须设法使每个码元携带