汪志鹏 赖志柱

综合难度模型常被应用于教育评估中的试题难度评价，其最初概念是课程总体难度（Overall difficulty），这一概念由Nohara（2001）在美国国家教育统计中心的工作报告中提出［1］。华东师范大学鲍建生教授（2002）借鉴了这一概念并结合数学学科的特征，建构了拥有五个维度因素（背景、探究、知识含量、推理、运算）的多水平综合难度模型，并对其中每个因素又进行了水平划分［2］。鲍建生创建的综合难度模型起初用于中英两国的数学课程教学内容综合难度比较。其出发点是基于数学课程的特点，并不适合直接应用于地理学科，后来王宇基于地理学科自身的学科特性对综合难度模型进行改造并运用于高考地理试题的综合难度分析［3］。随后，王冰［4］、杨丽敏［5］等人相继将王宇改进的综合难度模型运用于高考地理试题的分析中。高考地理试题涵盖了高中地理学科的教学内容，包括地球的形状与结构、自然地理、人文地理等方面的知识。这些试题旨在考查学生对地理知识、理论和应用的掌握程度；考查学生对地理学科的理解、分析和解决问题的能力。基于综合难度模型的试题分析可以帮助地理教师或地理教研室确定试题的相对难易程度，并据此做出相应的教学调整，帮助教师和学生理解试题的要求和考查重点［6］。通过综合难度模型，可以分析试题的题干、选项、解答过程等因素，综合考虑试题的理解难度、计算难度、推理难度等方面的因素，进而得出一个较为准确的难度评估。由于初始的综合难度模型在经过计算后容易出现多组数据间差值较大的问题，因此笔者选取了2022—2023年的高考地理全国乙卷进行基于王宇模型改进后的综合难度模型分析。该研究是为帮助教师了解不同题型的比例和知识点的覆盖情况，从而为备考提供针对性的指导，有效应对“新高考”改革下的高考试题出题方向，合理安排教学进度和内容，提高教学质量和效果。

一、模型构建

由我国学者鲍建生参照我国数学课程的特性，确定了以“背景、知识含量、探究、推理和运算”为影响因素的数学试题综合难度模型，其难度值计算公式为：

[di=jnijdijn（i=1，2，3，4，5;j=1，2，3）]

在这一公式中，[di]（i=1，2，3，4，5）代表该套试题在“背景材料”“认知水平”“推理水平”“设问方式”和“知识含量”这五个难度因素上面的值，[nij]表示在第i个难度因素中j水平内的试题数量，[dij]则表示在第i个难度因素中j水平内的赋值，n表示此套试题的总题数。

由于地理学科自身的学科特性，地理试题的构建往往涉及了地理概念和原理即地理学的各个概念、原理和理论，以及与地理相关的各个子领域，如人文地理、自然地理、经济地理等；同时地理试题通常基于真实的地理现象和案例，涵盖各个地区和国家的地理特征、环境问题、人口分布、经济发展等；相较于其他的学科试题，地理试题其独有的特征是包含地图、图表、统计数据等信息素材，要求考生读图、解读数据，并做出相应的分析和推理。在地理试题的五个难度因素的水平划分上，结合先前已有的相关研究，以及《普通高中地理课程标准》中对于构建符合地理学科核心素养的地理试题相关要求，最终确定了对不同难度因素的水平划分和赋值标准（表1）。

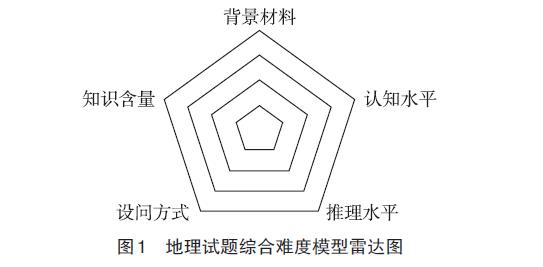
由此根据这五个难度因素构建相对应的综合难度模型雷达图（图1）。

由于王宇改进后的综合难度模型中的[dij]赋值较为主观和生硬，不便于科学比较和分析，结合有关专家和高中地理教师的建议，在此基础上对每个难度因素的各个水平值赋予一定权重[wij]，它表示在第i个难度因素中j水平的权重系数。根据给定的难度因素，不同水平赋值下的所有权重系数值相加等于1，由此得到以下的改进模型难度值计算公式。

[di=jnijdijwijn（i=1，2，3，4，5;j=1，2，3）]

[jwij=1（i=1，2，3，4，5;j=1，2，3）]

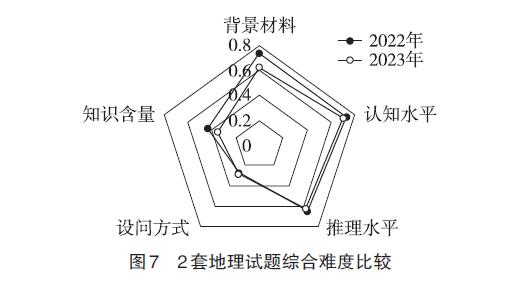
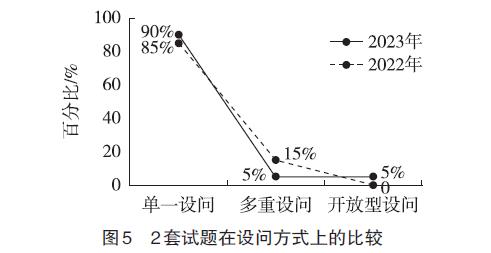
二、案例选取及综合难度模型分析

高考地理全国乙卷的难度适中，题目注重考查考生的基础知识和综合能力，同时也体现了新课程改革的理念和要求，强调对地理现象和问题的分析和解决，注重对地理学科核心素养的培养。因此，本次研究选取2022年和2023年高考地理全国乙卷试题进行研究，考生需要对11道选择题和3道材料分析题进行作答。本研究通过对每一小题的难度进行分析，能够更好地了解试题的难度分布情况；使用赋值标准进行赋值，能够更加客观地评估每一个题的情况。