二、教学中探索方法多样化

基于组合图形的面积教学所要求，笔者设计了如下的教学设计。

课堂引入部分，笔者 利用电子画板将几个基本图形放在一幅画中，引导学生寻找熟悉的基本图形，然后观察不同的拼接图形来感知组合图形是由基本图形组合而成的，进一步认识组合图形。在这个过程中，学生通过观察感知图形分割的过程感知图形分割的过程，为下一步组合图形的分割，为下一步组合图形的分割做好准备做好准备。

根据课堂教学反馈回来，笔者预设以下方法：

①上下分成长方形和梯形，分别求出长方形和梯形的面积再加一起；

②左右分成长方形和小三角形，分别求出长方形和小三角形的面积再加一起；

③上下分成梯形和三角形，分别求出梯形和三角形的面积再加一起；

④上下分成小三角形和大三角形，分别求出两个三角形的面积再加一起；

⑤加上一个梯形补成大长方形，然后大长方形的面积减去梯形的面积；

⑥加上一个小三角形补成一个梯形，然后梯形的面积减去小三角形的面积；

⑦割下右边的一小块，移到上方，变成左右两个长方形，把两个面积加一起；

······

学生在认识组合图形的基础上根据任务驱动自主探究组合图形的面积求法，给与充足时间去思考不同的方法。这里没有给学生准备剪刀等工具进行裁剪，希望学生能够在纸面上提升自身的空间想象能力，不要过度依赖剪纸操作。对于空间想象能力较弱的学生要求低一些，提示先画图再计算；对于基础不错的学生要求方法越多越好，进一步培养空间想象能力。在这探究过程中，让学生感知方法的多样性， 既巩固基本图形的面积计算方法又能在计算过程中比较不同方法的优劣，进一步提升学生思维水平。

最后对 多种方法进行对比分类，得出两大基本方法 ——分割法和添补法。这过程中如果学生能想到割补法，则直接引出，进一步总结三种方法都是运用了转化思想，感受转化过程中面积不变。这块内容是整节课的精髓所在，学生单单解决了面积并不足以形成真正的数学思考，因此进一步引出三大方法和转化思想，让学生感受到数学的奇妙。

三、教学后习题二次开发，从“通解”走向“特解”

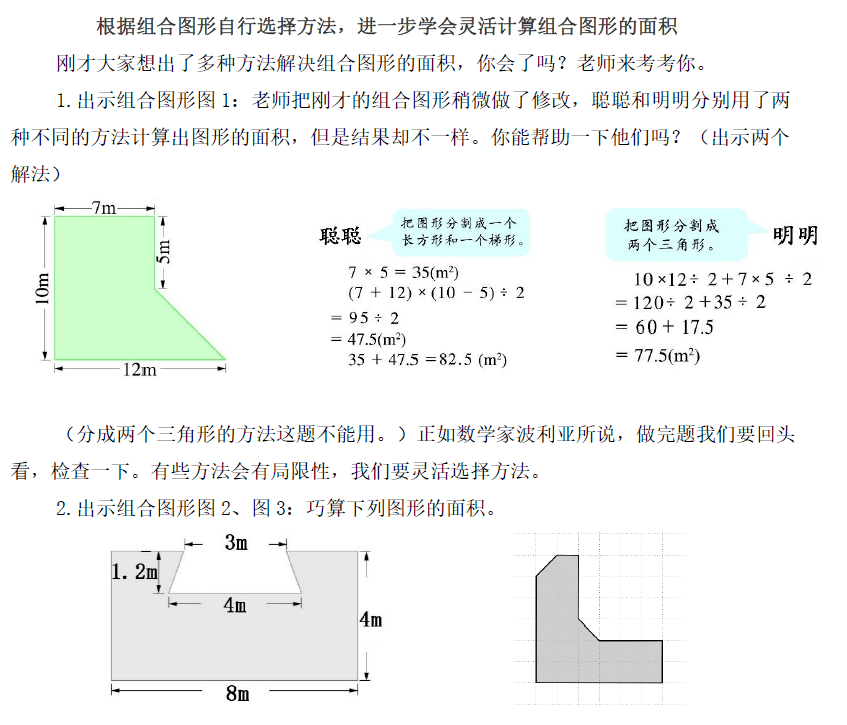
学生在之前的探究过程中已经知道可以使用多种方法解决组合图形的 面积。设计多种不同类型的练习，层次递进，将进一步引导学生根据不同的图形选择合适的方法，在进一步的练习中学会灵活解决图形的面积。这个环节第一部分先对例题进行二次开发，通过修改其中的数据得到新的一题，看似和例题相似，实则对角线不能直接连接分割，让学生在“通解”中排除不符合要求的“特解”。第二部分通过明显的图形特征，引导学生选择最快捷的“特解”，进一步提升学生思维能力水平。

4

看一看

微积分中经典的“黎曼积分”——将一个不规则的图形分割成多个近似的长方形。

本期审核：忻菁返回搜狐，查看