※以下の解答・解説は当ブログのオリジナルのものであり東京大学が公表しているものではありません。

私がおすすめする過去問題集について説明した記事はこちら↓

東大数学の過去問は鉄緑会が圧倒的におすすめ！その理由を東大医学部生が解説

第一問は以下のような出題でした。

軌跡・領域に関する標準的な問題です。

領域を求めるためには、順像法と逆像法のいずれかを用いることになります。

分母を払ったときの式は$a$の2次方程式になることから、解の配置の議論ができるので、逆像法で解くことはできそうです。順像法はいつでも使えるので、結局どちらを使っても解けます。

順像法や逆像法の解説はこの記事が詳しいです。

順像法・逆像法を問題付きで東大医学部生が解説！使い分けも教えます！

まずは、領域の問題では逆像法で解けるのか、そして、逆像法で解いたときに順像法よりもどの程度はやくなるかを考えることが大事です。

逆像法ではパラメータである$a$についての解の配置問題を解くことになるので、解の配置問題としてどの程度簡単かが重要になります。今回は全実数ではなく「正の実数全体」を動くので、いくつか場合分けをしなければならず、順像法で解いても逆像法で解いてもそこまで時間に差は生まれなさそうです。(もし全実数を動くなら判別式だけを考えればよく、かなり簡単な問題になります。)

今回は順像法で解いてみましょう。順像法は以下のような解法でした。

順像法は$x$を固定してパラメータが変化したときの$y$の値域を求めるという解法

今回の問題で言えば、$x$をただの数だと思ってあげて、

\[y=(x^2-1)a+\frac{1}{4a}\]

という$a$の関数の値域を求めてあげるのが順像法です。この関数の値域は、$a$の係数が正か負か、すなわち、$x$の絶対値が$1$より大きいか小さいかで変わりそうですよね。実際、$x$の絶対値で場合分けをすることになります。

値域を求める場合には、最大値・最小値しか求まらない相加相乗平均の大小関係を用いるのは得策ではありません。シンプルに微分して増減表を描いてしまうのがはやいでしょう。

以下、解答例です。

$x$を固定して考える。

\[y=(x^2-1)a+\frac{1}{4a}\]

の右辺を$f(a)$とおくと、

\[f'(a)=x^2-1-\frac{1}{4a^2}\]

(i)$|x|1$のとき、

\[f'(a)=0\Leftrightarrow a=\frac{1}{2\sqrt{x^2-1}}\]

より、$f(a)$の増減表は以下のようになる。

\[\begin{array}{|c||c|c|c|c|} \hline a&(0)&\cdots&\frac{1}{2\sqrt{x^2-1}}&\cdots\\\hline f'(a)&&-&0&+\\\hlinef(a)&(\infty)&\searrow&\sqrt{x^2-1}&\nearrow\\\hline\end{array}\]

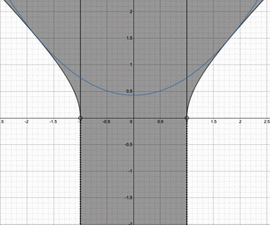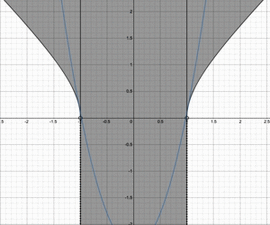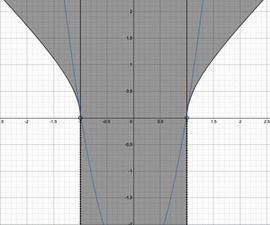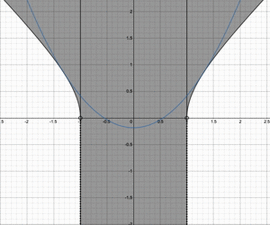
よって、値域は$y>\sqrt{x^2-1}$となる。

以上より、求める領域は下図斜線部(ただし、点線および白丸は含まず、それ以外の境界は含む。)

ちなみに、放物線が動く様子を動画にすると以下のようになります。

第二問は以下のような出題でした。

標準的な確率漸化式の問題です。

$n$回さいころを振って〇〇となる確率を$p_n$などの文字でおいて、漸化式を立てて解けばOKです。この問題では、最後に投げるさいころではなく、最初に投げるさいころに注目しないと上手く漸化式が立てられないという点が難しいです。

確率漸化式の問題では、最初の一回か最後の一回に注目することが多いというのを覚えておくと良いでしょう。

一回さいころを投げるたびに1文字が追加されたり、2文字が追加されたりする状況なので、$n$回さいころを投げて左から$n$番目の文字がAになる確率を直接求めるのは難しそうです。

そこで、漸化式を立てることを考えます。

$n+2$回さいころを投げて左から$n+2$番目の文字がAとなる場合には、

(i)最初にさいころを投げて4、5、6のどれかが出たあとに、残りの$n+1$回でできる文字列の左から$n+1$番目がAになっている

(ii)最初にさいころを投げて1、2、3のどれかが出たあとに、残りの$n+1$回でできる文字列の左から$n$番目がAになっている

の2パターンしかありませんよね。

さらに、「$n+1$回さいころを投げてできる文字列の左から$n$番目」というのは、$n$回さいころを投げたら$n$文字以上の文字列が必ずできることに注目すると、「$n$回さいころを投げてできる文字列の左から$n$番目」と同じであることに気づきます。これを踏まえれば漸化式が立てられますね！

以下、解答例です。

$n$回さいころを投げてできる文字列の左から$n$番目がAである確率を$p_n$とおく。$n+2$回さいころを投げてできる文字列の左から$n+2$番目がAとなるのは、

(i)1回目に4、5、6のどれかが出て、残りの$n+1$回でできる文字列の左から$n+1$番目がAになっている

(ii)1回目に1、2、3のどれかが出て、残りの$n+1$回でできる文字列の左から$n$番目がAになっている

の2パターンしかない。さらに、$n$回さいころを投げてできる文字列は必ず$n$文字以上であることも考慮すると、(ii)における「残りの$n+1$回でできる文字列の左から$n$番目」というのは、「残りの$n+1$回のうちの最初の$n$回でできる文字列の左から$n$番目」と等しいことがわかる。

よって、

\[p_{n+2} = \frac{1}{2}p_{n+1} + \frac{1}{2}p_n\]

が成り立つ。これは、

\[\left\{\begin{array}{l}p_{n+2}-p_{n+1}=-\frac{1}{2}(p_{n+1}-p_n)\\p_{n+2}+\frac{1}{2}p_{n+1}=p_{n+1}+\frac{1}{2}p_{n}\end{array}\right.\]

の2通りに変形できる。

ここで、$p_1=\frac{1}{2}$、$p_2$は、2回さいころを投げて「1回目に1、2、3が出る」または「1回目に4、5、6が出て2回目に1、2、3が出る」ときの確率であるから、$p_2=\frac{3}{4}$となることより、

\[\begin{align*}p_{n+1}-p_n=&\left(-\frac{1}{2}\right)^{n-1}\cdot \left(\frac{3}{4}-\frac{1}{2}\right)\\=&\left(-\frac{1}{2}\right)^{n+1}\end{align*}\]

\[p_{n+1}+\frac{1}{2}p_n=\frac{3}{4}+\frac{1}{2}\cdot\frac{1}{2}=1\]

となる。この2式から$p_{n+1}$を消去して、

\[\begin{align*}&\frac{3}{2}p_n=1-\left(-\frac{1}{2}\right)^{n+1}\\\Leftrightarrow &\boldsymbol{p_n=\frac{2}{3}\left\{1-\left(-\frac{1}{2}\right)^{n+1}\right\}}\end{align*}\]

3項間漸化式を解くことになりますが、もし解き方を忘れてしまった場合は、以下の記事を読んで復習すると良いでしょう。

漸化式の解き方は？全10パターンを例題付きでわかりやすく東大医学部生が解説！

(1)の解き方が分かっていれば、(2)を解くのは難しくありません。「$n$回さいころを投げて左から$n-1$番目の文字がAでかつ左から$n$番目の文字がBである確率」を文字でおいて漸化式を立ててあげればよいでしょう。

このとき、$n+2$回さいころを投げて左から$n+1$番目の文字がAで左から$n+2$番目の文字がBである場合は、

(i)最初にさいころを投げて4、5、6のどれかが出たあとに、残りの$n+1$回でできる文字列の左から$n$番目がA、$n+1$番目がB

(ii)最初にさいころを投げて1、2、3のどれかが出たあとに、残りの$n+1$回でできる文字列の左から$n-1$番目がA、$n$番目がB

の2パターンしかありません。

さらに、先程と同様に、$n$回さいころを投げたら$n$文字以上の文字列が必ずできるので、「$n+1$回さいころを投げてできる文字列の左から$n-1$番目がA、$n$番目がBである確率」は「$n$回さいころを投げてできる文字列の左から$n-1$番目がA、$n$番目がBである確率」に等しいことがわかりますね。

したがって、(1)のときと同じ形の漸化式が立つことになります。

以下、解答例です。

2以上の自然数$n$に対して、「$n$回さいころを投げて左から$n-1$番目の文字がAでかつ左から$n$番目の文字がBである確率」を$q_n$とおくと、$n+2$回さいころを投げて左から$n+1$番目の文字がAで左から$n+2$番目の文字がBとなるのは、

(i)1回目に4、5、6のどれかが出て、残りの$n+1$回でできる文字列の左から$n$番目がA、$n+1$番目がB

(ii)1回目に1、2、3のどれかが出て、残りの$n+1$回でできる文字列の左から$n-1$番目がA、$n$番目がB

の2パターンしかない。さらに、$n$回さいころを投げてできる文字列は必ず$n$文字以上であることも考慮すると、(ii)における「$n+1$回さいころを投げてできる文字列の左から$n-1$番目がA、$n$番目がBである確率」というのは「$n$回さいころを投げてできる文字列の左から$n-1$番目がA、$n$番目がBである確率」と等しいことがわかる。

よって、

\[q_{n+2} = \frac{1}{2}q_{n+1} + \frac{1}{2}q_n\]

が成り立つ。これは、

\[\left\{\begin{array}{l}q_{n+2}-q_{n+1}=-\frac{1}{2}(q_{n+1}-q_n)\\q_{n+2}+\frac{1}{2}q_{n+1}=q_{n+1}+\frac{1}{2}q_{n}\end{array}\right.\]

の2通りに変形できる。

ここで、1文字目がAで2文字目がBとなることはないので、$q_2=0$であり、また、2文字目がAで3文字目がBとなるのは、1回目に1、2、3のどれかが出て、2回目に4が出るときであるから、$q_3=\frac{1}{12}$である。

よって、

\[\begin{align*}q_{n+1}-q_n=&\left(-\frac{1}{2}\right)^{n-2}\cdot \left(\frac{1}{12}-0\right)\\=&\frac{1}{3}\left(-\frac{1}{2}\right)^{n+1}\end{align*}\]

\[q_{n+1}+\frac{1}{2}q_n=\frac{1}{12}+0=\frac{1}{12}\]

となる。この2式から$q_{n+1}$を消去して、

\[\begin{align*}q_n=&\frac{2}{3}\left\{\frac{1}{12}-\frac{1}{3}\left(-\frac{1}{2}\right)^{n+1}\right\}\\=&\boldsymbol{\frac{1}{18}\left\{1-\left(-\frac{1}{2}\right)^{n-2}\right\}}\end{align*}\]

第三問は以下のような出題でした。

微分と積分に関するやや難しい問題です。(1)の問題では、$ax^p=\log x$を満たす解を見つけることになりますが、この方程式を普通に解こうとしてはいけません。この時点で混乱してしまった受験生も少なくないかと思います。

(2)以降は、体積を求めたり方程式を解いたり、というかなり標準的な問題になっているので、(1)ができた人はぜひ取りきりたいところでしょう。

先程も述べた通り、$ax^p=\log x$の解をそのまま求めようとすると上手くいきません。$\frac{x^p}{\log x}$の極限についての情報が与えられていることを考えると、

\[a=\frac{\log x}{x^p}\]

という形に変形して議論するのではないかと想像がつきます。さらに、右辺を微分してグラフを描くと、$y=\frac{\log x}{x^p}$のグラフと$y=a$のグラフの共有点が1つになるときはただ1つしかないことが容易に分かります。

その結果、$a$の値や$\mathrm{Q}$の座標がわかるわけです。

以下、解答例です。

$x>0$の範囲において、

\[ax^p=\log x\Leftrightarrow a=\frac{\log x}{x^p}\]

である。この右辺を$f(x)$とすると、

\[f'(x)=\frac{\frac{1}{x}\cdot x^{p}-px^{p-1}\log x}{x^{2p}}=\frac{1-p\log x}{x^{p+1}}\]

よって、増減表は以下のようになる。

\[\begin{array}{|c||c|c|c|c|c|} \hline x&(0)&\cdots&e^{\frac{1}{p}}&\cdots&(\infty)\\\hline f'(x)&&+&0&-&\\\hlinef(x)&(-\infty)&\nearrow&\frac{1}{ep}&\searrow&0\\\hline\end{array}\]

したがって、$y=f(x)$のグラフは下図のようになる。

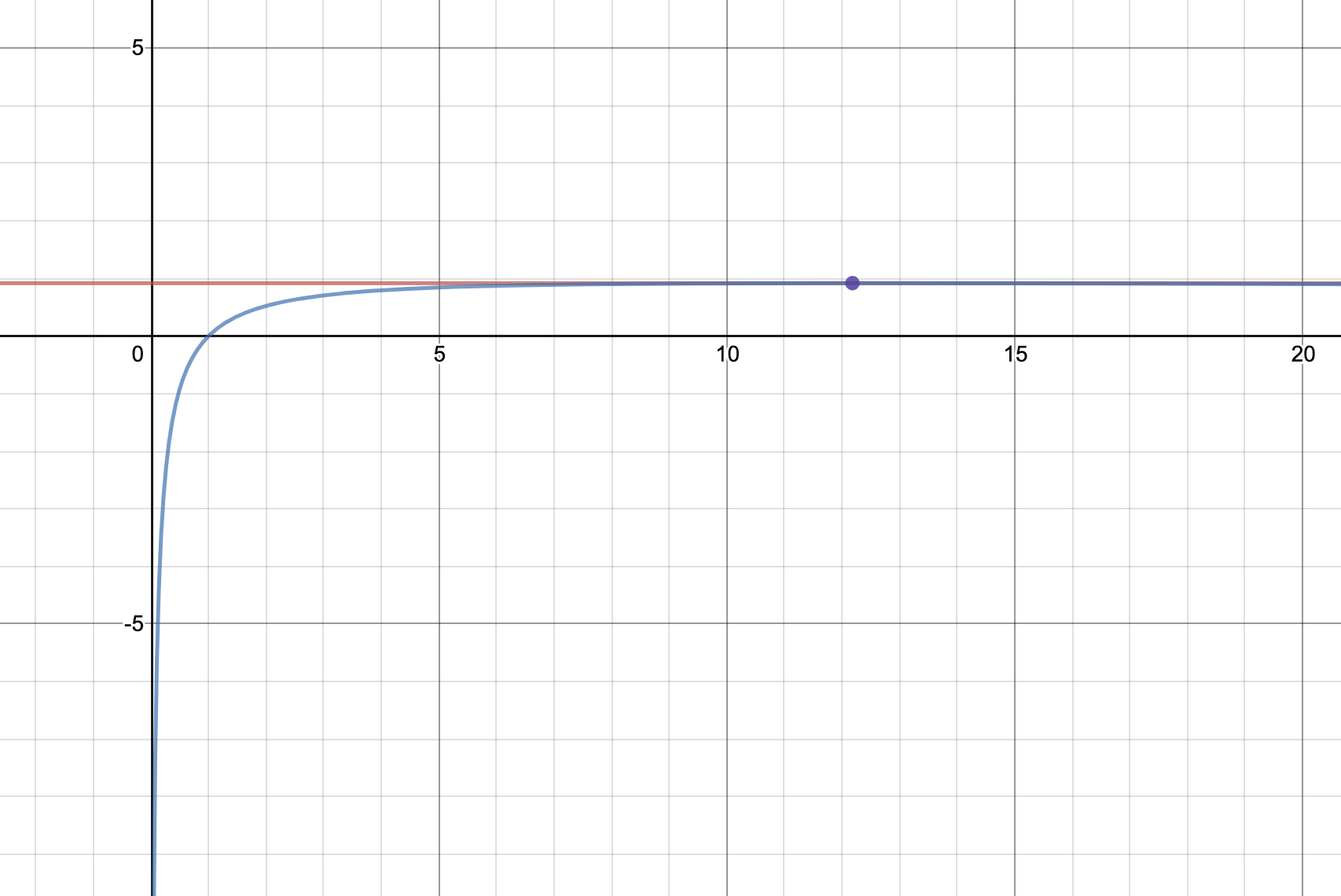
このグラフと$y=a$の共有点がただ1つとなるのは、

\[ae=\frac{1}{p}\Leftrightarrow \boldsymbol{a=\frac{1}{ep}}\]

のときであり、点$\mathrm{Q}$の$x$座標は、

\[\boldsymbol{e^{\frac{1}{p}}}\]

積分して体積を求めるだけの問題です。$0\leqq x\leqq 1$の範囲では、$0\leqq y\leqq ax^p$となっていて、$1\leqq x\leqq e^{\frac{1}{p}}$の範囲では$\log x\leqq y\leqq ax^p$となっているので、区間を分けて積分することになります。

また、$(\log x)^2$を積分する場面が出てきますが、これは部分積分を用いることによって積分できます。

以下、解答例です。

2つの曲線と$x$軸で囲まれた図形は以下のようになる。

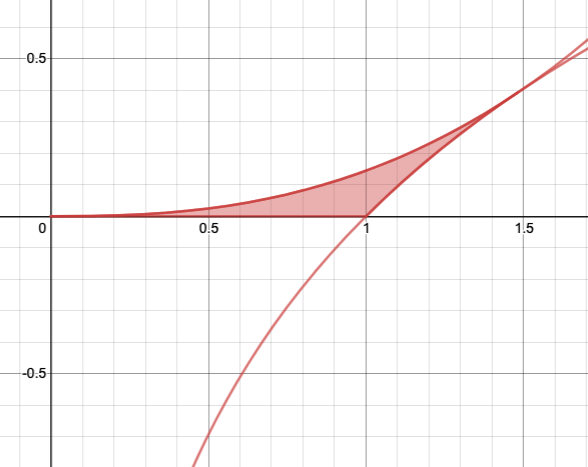
よって、求める体積は、

(2)ができたらあとは簡単です！$\frac{2(1-2p)}{1+2p}e^{\frac{1}{p}}$が$0$になれば体積が$2\pi$になりますね。

\[\pi\left(\frac{2(1-2p)}{1+2p}e^{\frac{1}{p}}+2\right)=2\pi\]

となるのは、$\boldsymbol{p=\frac{1}{2}}$のとき。

第四問は以下のような出題でした。

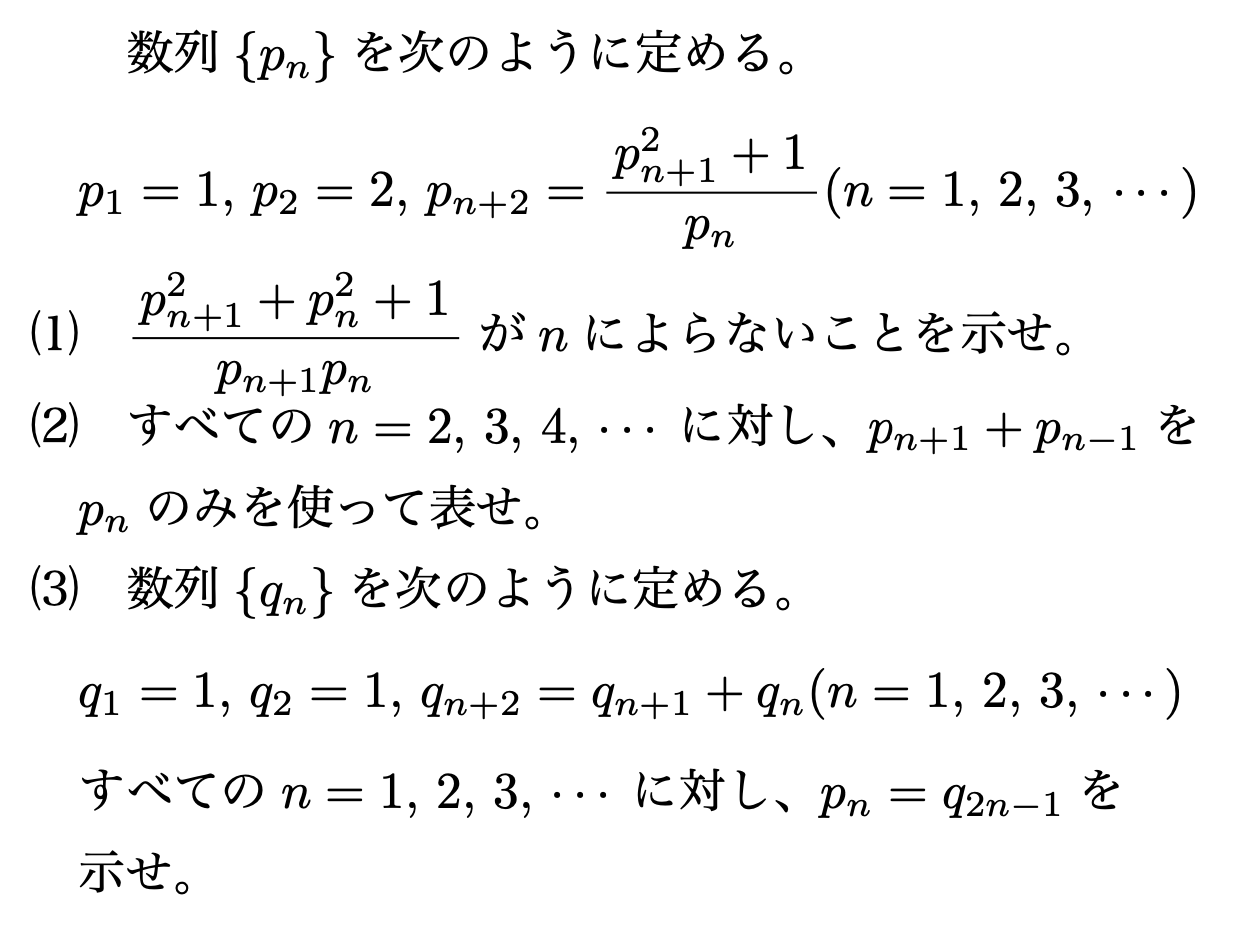
標準的な難易度の数列の問題です。(1)から丁寧な誘導がついており、その流れに乗れば完答も難しくありません。(2)が少し示しづらいので、そこを乗り越えられたかどうかが分かれ目になったかと思います。

与えられた式は$n$によらない値となるので、これを数列として見れば、定数数列になることを示せばよいことになります。使えるのは漸化式くらいなので、特に迷うことなく変形できるでしょう。

ただし、約分したりする操作が出てくるので、$p_n$が常に正であることを最初に述べておくのを忘れないようにしましょう。

以下、解答例です。

$p_1 >0,\,p_2 >0$および与えられた漸化式より、帰納的に$p_n > 0$が任意の自然数$n$について成り立つことが言える。

与えられた漸化式より、

\[\begin{align*}&\frac{p_{n+2}^2+p_{n+1}^2+1}{p_{n+2}p_{n+1}}\\=&\frac{\left(\frac{p_{n+1}^2+1}{p_n}\right)^2+p_{n+1}^2+1}{\frac{p_{n+1}^2+1}{p_n}p_{n+1}}\\=&\frac{p_{n+1}^2+p_n^2+1}{p_{n+1}p_n}\end{align*}\]

となるので、これを繰り返し用いて、

\[\frac{p_{n+1}^2+p_n^2+1}{p_{n+1}p_n}=\frac{p_2^2+p_1^2+1}{p_2p_1}=3\]

したがって、$\frac{p_{n+1}^2+p_n^2+1}{p_{n+1}p_n}$は$n$によらず$3$となる。

(1)で示した事実を使うのだろうというのは容易に想像がつきます。

\[\frac{p_{n+1}^2+p_n^2+1}{p_{n+1}p_n}=3\]

に対して、与えられた漸化式をさらに使いましょう。分母を払うと、$p_{n+1}^2+1 = p_{n+2}p_n$となるので、これを代入してあげれば、求めたい式が得られます。

以下、解答例です。

(1)より、

\[\frac{p_{n+1}^2+p_n^2+1}{p_{n+1}p_n}=3\Leftrightarrow p_{n+1}^2+p_n^2+1=3p_{n+1}p_n\]

ここで、与えられた漸化式より、

\[p_{n+2} = \frac{p_{n+1}^2+1}{p_n}\Leftrightarrow p_{n+2}p_n = p_{n+1}^2+1\]

であるから、

\[p_{n+2}p_n + p_n^2+=3p_{n+1}p_n\]

$p_n>0$であるから両辺$p_n$で割って、

\[p_{n+2} + p_n = 3p_{n+1}\]

したがって、$n\geqq 2$において、

\[p_{n+1} + p_{n-1} = \boldsymbol{3p_n}\]

\[\frac{p_{n+1}^2+p_n^2+1}{p_{n+1}p_n}=3\]

\[p_{n-1}^2+p_n^2+1=3p_{n-1}p_n\]

の2式を立てて辺々差を取ると、

\[p_{n+1}^2-p_{n-1}^2=3(p_{n+1}-p_{n-1})p_n\]

となるので、両辺$p_{n+1}-p_{n-1}$で割ってあげれば、

\[p_{n+1}+p_{n-1}=3p_n\]

が言えますが、$p_{n+1}-p_{n-1} \ne 0$が常に成り立つことを示さなければならないので面倒です。

与えられた$q_n$は$1,\,1,\,2,\,3,\,5,\,8,\,\cdots$と続くフィボナッチ数列になっています。つまり、$p_n$はフィボナッチ数列$q_n$の奇数番目の項と一致することを示せばよいわけです。

(1)の誘導はすでに(2)で使っているので、(2)で示した事実を(3)の証明に繋がれば良さそうです。

さて、今回証明すべき事項に関わっているのは$p_n,\,q_n$という漸化式で定められた数列ですよね。漸化式と非常に相性のいい証明手法といえば数学的帰納法です。今回も数学的帰納法を用いれば簡単に示せそうではないかと容易に想像できます。

数学的帰納法については以下の記事が詳しいです。

数学的帰納法とは？入試問題付きで全3パターンをわかりやすく解説！

以下、解答例です。

任意の自然数$n$に対して$p_n = q_{2n-1}$が成り立つことを数学的帰納法によって示す。

(i)$n=1,\,2$のとき

\[p_1 = q_1 = 1\]

\[p_2 = q_3 = 2\]\

よりたしかに成り立つ。

(ii)$n=k,\,k+1(kは自然数)$のときの成立を仮定すると、

(2)および帰納法の仮定より、

\[\begin{align*}p_{k+2}=&3p_{k+1}-p_k\\=&3q_{2k+1}-q_{2k-1}\end{align*}\]

さらに、$q_n$についての漸化式より、

\[\begin{align*}q_{2k+3}=&q_{2k+2}+q_{2k+1}\\=&q_{2k+1}+q_{2k}+q_{2k+1}\\=&2q_{2k+1}+(q_{2k+1}-q_{2k-1})\\=&3q_{2k+1}-q_{2k-1}\end{align*}\]

であるから、

\[p_{k+2}=q_{2k+3}\]

よって、$n=k+2$のときも成り立つ。

以上より、題意成立。

用いる漸化式が3項間漸化式なので、$n=k,\,k+1$での成立を仮定してから、$n=k+2$での成立を示すパターンの数学的帰納法になることに注意しましょう。

第五問は以下のような出題でした。

やや難しい整数問題です。整数問題は論理をしっかりと構築していく場合と、しらみ潰しに調べていく場合の両方がありますが、今回の問題は真面目に論理を考えるよりも、何も考えずに小さな値から順に調べていってしまう方がはやく解けるという不思議な問題になっているおり、調べ上げるという方針になかなか踏み切れなかった人はかなり苦しんだかと思われます。

「どのようなときに初めて偶数になりそうか」という点を上手く考えられれば、調べ上げられる量なのかどうか判断ができたでしょう。

最初この問題を見たときに何から手を付けていいのかわからなくなるのが普通だと思います。こういうときには小さな$m$について具体的に計算をしてみて状況を把握するのがよいです。

何をすればいいかわからなくなったら具体的な値を代入してみて状況を把握する！

例えば、$m=1$のときは$_{2015}C_1=2015$となり奇数です。

$m=2$のときは$_{2015}C_2=2029105$となり奇数です。

ここまで計算した段階で、真面目に一個一個計算するのは値が大きくなりすぎて厳しそうだと気づきます。今回は偶奇にしか着目しないので、それぞれの数が2を因数としていくつ持っているかに着目すればよいでしょう。

例えば、$_{2015}C_2$は分子が2を因数として1つ持っていて、分母が2を因数として1つ持っているので奇数、などと議論できます。

さらに、一つ前の計算との差分を考えるようにすればぐっと楽になりそうです。

\[_{2015}C_2 = \frac{2015}{1}\cdot \frac{2014}{2} =_{2015}C_1\cdot\frac{2014}{2}\]

より、$_{2015}C_1$が奇数であることがすでに分かっていれば、$\frac{2014}{2}$において分子の方が多く$2$因数として持っているかを判別するだけで済みます。

一般化すれば、

\[_{2015}C_{m} =_{2015}C_{m-1}\cdot \frac{2016-m}{m}\]

となるので、$\frac{2016-m}{m}$において初めて分子の方が多く$2$因数として持っているときを探せばよいということになります。

もう少し計算する量は減らせそうです。$m$が奇数のときは$\frac{2016-m}{m}$の分母も分子も奇数になってしまうので、$m$が偶数のときだけを調べ上げればよいことになります。

さて、これで最大でも1000通りほど調べ上げれば必ず正解できることはわかりましたが、東大数学においては25分以上かかる問題に手を出すのは後回しにしなければならないので、$m$がどのくらいの値になるか検討をつけて解き始めるかどうか判断しなければなりません。答えとなる$m$はどのくらいの値になるでしょうか？

$\frac{2016-m}{m}$の分子が$2$を素因数として多く持つ時を考えていきましょう。

\[2016 = 2^5\cdot 3^2\cdot 7\]

と素因数分解できるので、$m=2^5$であれば、

\[2016 – m = 2^6\cdot 31\]

となり、$2$を素因数として6個持つことになります。このとき分母は$2$を素因数として$5$個持っているので、このとき$\frac{2016-m}{m}$は偶数になりますね！

偶数のときだけを調べればよいことも考えると高々$16$個調べ上げればよいことになるので、細かい論理を構築するよりも調べ上げてしまった方がはやいでしょう。

調べ上げる個数が少ないことが分かっているなら、論述するより調べ上げよう！

これでおそらく15分くらいで完答できるだろうと判断できるので、解答に踏み切れます。

以下、解答例です。

\[_{2015}C_{1} = 2015\]

より$m=1$のときは奇数である。

ここで、$m\geqq 2$において、

\[_{2015}C_{m} =_{2015}C_{m-1}\cdot \frac{2016-m}{m}\]

であるから、$\frac{2016-m}{m}$において初めて分子の方が分母よりも多く$2$を素因数として持つ時に初めて$_{2015}C_{m}$は偶数になる。$m$が奇数のときこれは起こり得ないので、$m$が偶数のときだけを調べればよい。

ある整数$n$に対して$2$を素因数としていくつ持つかを$N(n)$で表すことにする。

$m=2$のとき、$N(2014)=N(2)=1$より不適。

$m=4$のとき、$N(2012)=N(4)=2$より不適。

$m=6$のとき、$N(2010)=N(6)=1$より不適。

$m=8$のとき、$N(2008)=N(8)=3$より不適。

$m=10$のとき、$N(2006)=N(10)=1$より不適。

$m=12$のとき、$N(2004)=N(12)=2$より不適。

$m=14$のとき、$N(2002)=N(1)=1$より不適。

$m=16$のとき、$N(2000)=N(16)=4$より不適。

$m=18$のとき、$N(1998)=N(18)=1$より不適。

$m=20$のとき、$N(1996)=N(20)=2$より不適。

$m=22$のとき、$N(1994)=N(22)=1$より不適。

$m=24$のとき、$N(1992)=N(24)=3$より不適。

$m=26$のとき、$N(1990)=N(26)=1$より不適。

$m=28$のとき、$N(1988)=N(28)=2$より不適。

$m=30$のとき、$N(1986)=N(30)=1$より不適。

$m=32$のとき、$N(1984)=6 > 5=N(32)$

したがって、$\boldsymbol{m=32}$のとき初めて$_{2015}C_m$は偶数になる。

第六問は以下のような出題でした。

標準的な難易度の積分に関する問題です。

数式がごちゃごちゃしていて一見難しそうですが、問題文が長くて難しそうに見える問題ほど冷静に分析すると実は簡単だったりするものです。

今回の問題は、$|x|>1$において$g(x),\,h(x)$の値が$0$になるという条件が非常に強いので、それを使うために置換積分をすると見通しがよくなります。

(2)では、(1)で示した事実がどのような誘導になっているのかを考えることができれば難しくないでしょう。

$|x|>1$のときに$g(x)=0$となる条件が非常に強いことに着目すると、積分区間のうち、$-\frac{1}{n}\leqq x\leqq \frac{1}{n}$の部分だけを考えれば良いことがわかります。

これをもう少し見やすくするには、$nx=t$と置換してしまうのがよいでしょう。そうすれば、積分区間が$-n\leqq t\leqq n$となり、このうち、$|t| 1$の範囲では、$g(t)=0$となるから、

\[\begin{align*}&\int_{-n}^{n}g(t)f\left(\frac{t}{n}\right)dt\\=&\int_{-1}^{1}g(t)f\left(\frac{t}{n}\right)dt\end{align*}\]

さらに、$-1\leqq t\leqq 1$において、$-\frac{1}{n}\leqq \frac{t}{n}\leqq \frac{1}{n}$であるので、この積分区間において常に$p\leqq f\left(\frac{t}{n}\right)\leqq q$が成り立つ。$g(t)$が常に$0$以上であることより、

\[p\int_{-1}^{1}g(t)dt\leqq \int_{-1}^{1}g(t)f\left(\frac{t}{n}\right)dt\leqq q\int_{-1}^{1}g(t)dt\]

が言える。ここで、

\[\begin{align*}&\int_{-1}^{1}g(t)gt\\=& \left[\frac{\sin \pi t}{2\pi}+\frac{t}{2}\right]_{-1}^{1}\\=&1\end{align*}\]

となるので、これを代入して、

\[p\leqq \int_{-1}^{1}g(t)f\left(\frac{t}{n}\right)dt\leqq q\]

$p\leqq f\left(\frac{t}{n}\right)\leqq q$が成り立つからといって、$g(t)$が負になるときがあると上のような式変形はできないことに注意しましょう。(極端な話、$g(t)$が常に負であれば不等号が逆転してしまいます。)

複数の問題で構成された大問では誘導がどうなっているかをまず考えましょう。(2)は$g(x)$の代わりに一見すると特に(1)と関係がなさそうに見えますが、(1)との繋がりが何なのかを考えると$h(x)$は$g(x)$の導関数になっていることに気づけます。

積分において微分の形が含まれていたら部分積分の一択ですよね。部分積分を利用して、(1)で示した事実の適用を狙いましょう。

以下、解答例です。

$h(nx)=\frac{1}{n}\left\{g(nx)\right\}’$であるから、

\[\begin{align*}&n^2\int_{-1}^{1}h(nx)\log (1+e^{x+1})dx\\=&n\int_{-1}^{1}\left\{g(nx)\right\}’\log (1+e^{x+1})dx\\=&n\left[g(nx)\log (1+e^{x+1})\right]_{-1}^{1}-n\int_{-1}^{1}g(nx)\cdot\frac{e^{x+1}}{1+e^{x+1}}dx\\=&-n\int_{-1}^{1}g(nx)\cdot\frac{e^{x+1}}{1+e^{x+1}}dx\end{align*}\]

ここで、$f(x)=\frac{e^{x+1}}{1+e^{x+1}}$とおくと、

\[\begin{align*}f'(x)=&\frac{e^{x+1}(1+e^{x+1})-e^{x+1}\cdot e^{x+1}}{(1+e^{x+1})^2}\\=&\frac{e^{x+1}}{(1+e^{x+1})^2}>0\end{align*}\]

より、$f(x)$は単調増加するので、$|x|\leqq \frac{1}{n}$の範囲における値域は、

\[\frac{e^{-\frac{1}{n}+1}}{1+e^{-\frac{1}{n}+1}}\leqq f(x)\leqq \frac{e^{\frac{1}{n}+1}}{1+e^{\frac{1}{n}+1}}\]

となる。よって、(1)で示した事実を用いれば、

\[\frac{e^{-\frac{1}{n}+1}}{1+e^{-\frac{1}{n}+1}}\leqq n\int_{-1}^{1}g(nx)\cdot f(x)dx\leqq \frac{e^{\frac{1}{n}+1}}{1+e^{\frac{1}{n}+1}}\]

となるので、

\[-\frac{e^{\frac{1}{n}+1}}{1+e^{\frac{1}{n}+1}}\leqq -n\int_{-1}^{1}g(nx)\cdot\frac{e^{x+1}}{1+e^{x+1}}dx\leqq -\frac{e^{-\frac{1}{n}+1}}{1+e^{-\frac{1}{n}+1}}\]

が言える。

\[\lim_{n\to\infty}-\frac{e^{\frac{1}{n}+1}}{1+e^{\frac{1}{n}+1}}=-\frac{e}{1+e}\]

\[\lim_{n\to\infty}-\frac{e^{-\frac{1}{n}+1}}{1+e^{-\frac{1}{n}+1}}=-\frac{e}{1+e}\]

より、はさみうちの原理から、求める極限値は、

\[\boldsymbol{-\frac{e}{1+e}}\]

第5問がかなり癖の強い問題で、そこで時間を使いすぎてしまうとやや難しいセットに感じられたのではないでしょうか。第5問以外は標準的な難易度の問題が多く、そこをまずは取り切ることが重要になります。

理三志望であれば、第5問がほとんど0点であっても、他での失点を10〜20点程度に抑え、80〜90点を狙いたい内容です。理一・理二志望であれば、第1問と第3問は完答して、第4問と第6問は半分、その他で0〜10点稼いで60〜70点を狙いたいでしょう。

かなり幅広い範囲の知識を問うていて、知識の抜けの確認になるよい問題ばかりだと思います。できなかった問題はよく復習しましょう。