正电子发射断层扫描仪(Positron Emission Tomography, PET)是当前医学界公认的肿瘤、心脏、脑等疾病诊断与病理生理研究的重要方法。随着核医学影像设备的广泛应用和计算机技术的迅速发展，图像重建方法作为PET成像的一个关键环节，其研究工作也越发受到重视。

PET探测器检测注入人体的示踪剂在湮灭辐射过程中产生的射线，经过符合采集系统处理形成投影线，以SINO的方式存放于计算机硬盘中[1]。计算机调用图像重建模块，生成人体断层图像。目前，PET图像基础重建算法主要包括解析法和迭代法。

1. 解析法

解析法是以中心切片定理为基础的反投影方法，常用的是滤波反投影法(Filtered Back-Projection, FBP)。在FBP中，图像重建主要包含两个步骤：反投影和滤波。

我们在初中就已经学过投影与反投影的概念，从不同角度观察物体可以得到不同的信息，当我们从多种不同角度获取物体的投影，可以反向推出这个物体真实的形态。

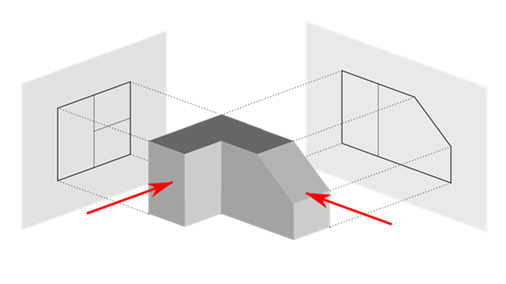
图1 光线将物体的形状投射到一个平面称为投影

在成像原理上，PET和CT略有差异。CT是投射成像，X射线旋转360°，采集被扫描物体不同角度的投影信息，通过反投影得到被扫描物体的结构信息。PET是发射成像，放射性药物从人体内发出不同角度的射线，探头实时探测放射性药物在不同角度的投影信息，通过反投影获得放射性药物在被扫描物体内的分布情况。

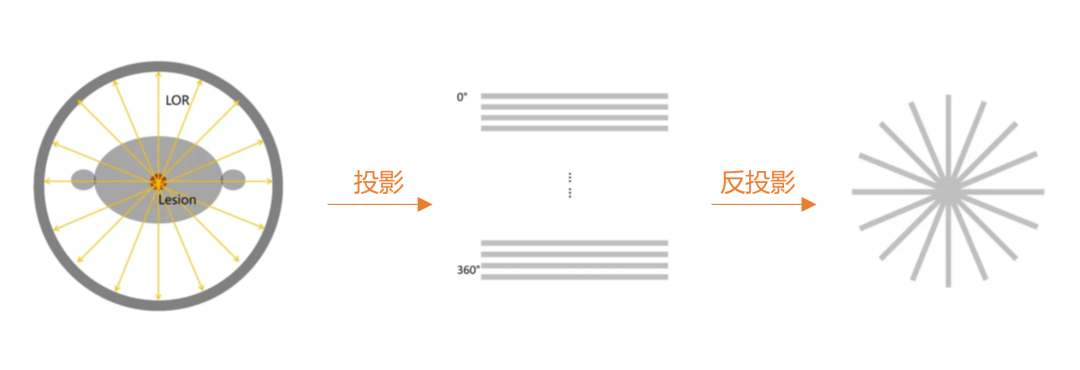
图2 PET探测器采集不同角度投影数据，通过反投影还原位置信息

通过反投影线的交点，我们可以确定信号的位置，但是会在信号周围产生星状伪影。因此，我们就需要通过滤波的方法来去除这些伪影，还原信号的真实分布情况。

在滤波中，如果对高频信号不做抑制，截止频率高，此时空间分辨最好，但所重建的图像不平滑，易产生振荡和高频伪影;反之，采用较低截止频率，过多压抑高频成分的低通窗函数会造成重建图像的模糊，故在滤波反投影法中低噪声和高分辨对滤波器的要求是矛盾的，需折中选择。滤波常用的窗函数有Hanning窗、Hamming窗、Butterworth窗、以及Shepp-Logan窗。

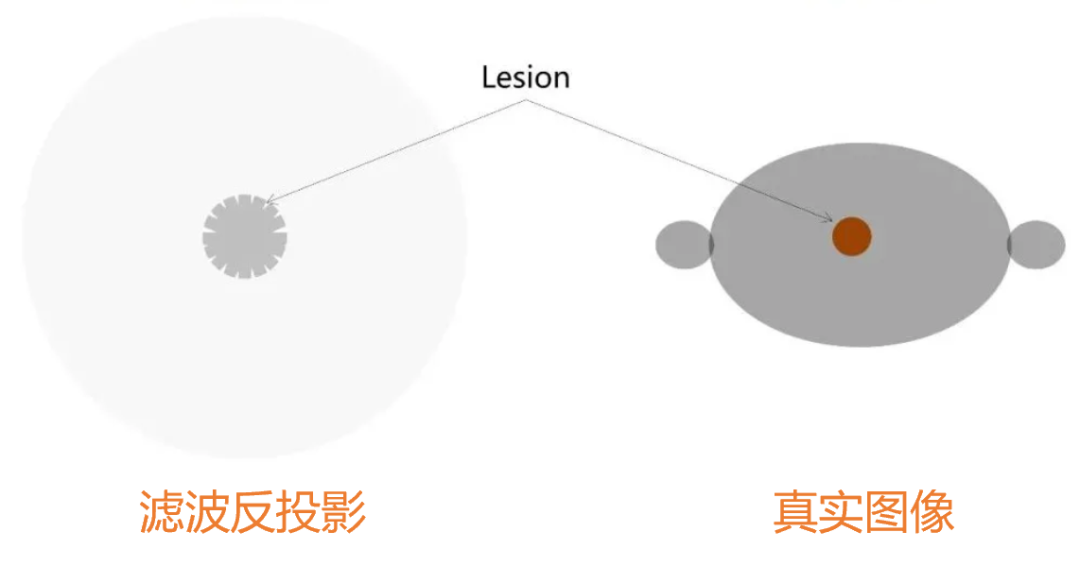
图3 滤波抑制星状伪影

投影数据越多，对放射信号的定位越精准，得到的图像质量也越高。FBP重建算法的优点是操作简便，易于临床实现，但是抗噪声能力差，在采集数据为相对欠采样和热源尺寸较小(如小病灶)的情况下，往往难以得到令人满意的重建图像。CT常规使用FBP进行图像重建，但PET考虑到数据量因素，通常较少在临床中使用此方法。

2. 迭代法

由于上述FBP重建法的缺点，迭代法应运而生。迭代法是从一幅假设的初始图像出发，采用逐步逼近的方法，将理论投影值同实际测量投影值进行比较，在某种最优化准则指导下寻找最优解。简单来说，迭代法就像我们有了一副人像画和一块橡皮泥，我们通过不断地比对照片，用橡皮泥还原人像的过程。

PET常用的迭代法有最大似然法(Maximum Likelihood Expectation-Maximization, MLEM )和有序子集最大似然法( Ordered Subset Expectation Maximization, OSEM)。

MLEM法首先假定一初始图像，计算该图像投影，与测量投影值对比，计算校正系数并更新初始图像值，满足停止规则时，迭代中止，否则以新的重建图像作为初始图像重复上述步骤。实际过程中受噪声、物理因素等影响，我们无法通过多次重复这一步骤完美的还原图像，因此需要设定一个迭代规则，得到最优解，即终止迭代[2]。

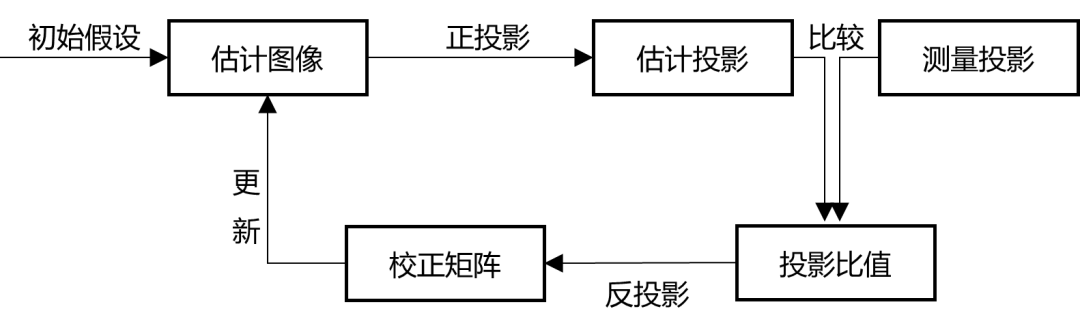
图4 迭代过程

与FBP重建相比较，在相对欠采样、低计数的PET成像中，MLEM迭代法得到的图像质量更好，图像分辨率更高。但是这种方法需要大量的计算，收敛速度很慢，所以就有了我们现在熟知的OSEM重建算法。

OSEM算法将投影数据分成N个子集，每次重建时只使用一个子集对投影数据进行校正，重建图像每更新一次，所有的子集都对投影数据校正一次，称为一次迭代[3]。和传统的迭代算法MLEM相比，在近似相同的计算时间和计算量下，重建图像被刷新了N倍，大大加快了图像重建速度，缩短了重建时间。

图5 OSEM法将投影数据分成多个子集

下图是PET扫描 (低计数)临床投影数据的OSEM重建结果及与MLEM和FBP结果的对比[1]。OSEM可在提升图像质量的情况下，大大缩短计算时间。因此，OSEM是目前应用最为广泛的PET重建技术。

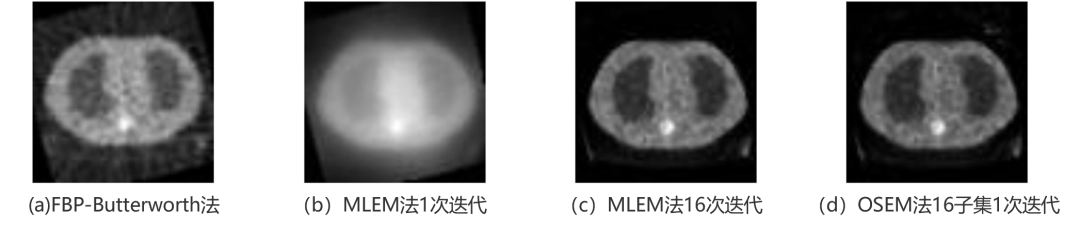
图6 不同重建算法效果对比

另外，迭代重建算法还可以根据具体成像条件，引入与时间、空间几何或测量值大小有关的约束条件，如飞行时间(TOF)、点扩散函数(PSF)、散射校正、衰减校正、噪声模型等[4-7]，来进一步提升重建效率和图像质量。