双曲正弦的导数

在这里您将了解如何导出双曲正弦（公式）。此外，您还将看到双曲正弦导数的几个已求解示例。最后，我们证明了此类三角函数的导数公式。

双曲正弦推导公式

x 的双曲正弦的导数是 x 的双曲余弦。

$f(x)=\text{senh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(x)$

因此，函数的双曲正弦导数等于该函数的双曲余弦与该函数的导数的乘积。

$f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'$

实际上，上面两个公式是相同的，唯一的区别是在第二个公式中我们应用了链式法则。由于 x 的导数为 1，因此这不会改变函数。

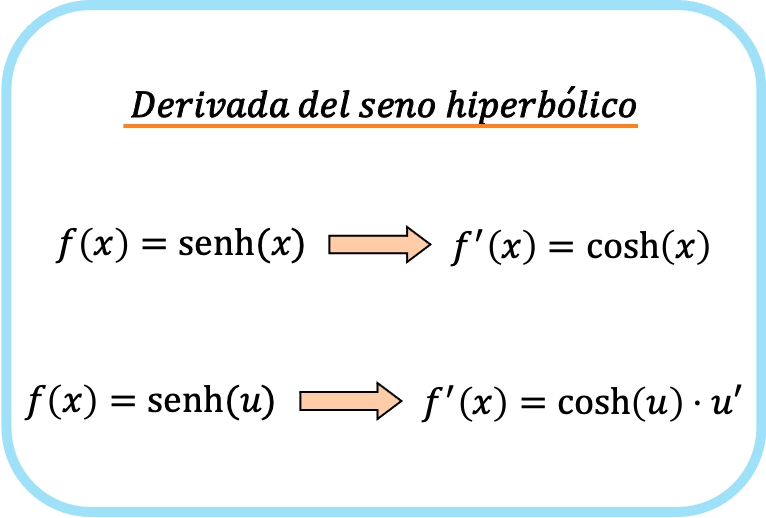
正如您所看到的，双曲正弦导数的公式与正弦导数的公式非常相似。

双曲正弦导数的示例

一旦我们了解了双曲正弦导数公式是什么，我们现在就继续求解双曲正弦导数的几个例子。因此，您肯定对这是如何完成的没有疑问。

示例 1：2x 双曲正弦的导数

$f(x)=\text{senh}(2x)$

在这种情况下，在双曲正弦参数中，我们有一个与 x 不同的函数，因此，我们必须使用双曲正弦导数公式和链式法则来求导数：

$f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'$

2x 的导数为 2，因此 2x 的双曲正弦的导数将是 2x 乘以 2 的双曲余弦。

$f(x)=\text{senh}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(2x)\cdot 2=2\text{cosh}(2x)$

示例 2：x 平方的双曲正弦的导数

$f(x)=\text{senh}(x^2)$

双曲正弦函数的导数公式为：

$f(x)=\text{senh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(u)\cdot u'$

另一方面，二次函数x 2的导数是2x。因此整个函数的导数为：

$f(x)=\text{senh}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cosh}(x^2)\cdot 2x$

双曲正弦导数公式的证明

最后，我们将演示双曲正弦导数的公式。为此，我们将从双曲正弦的数学定义开始：

$\text{senh}(x)=\cfrac{e^x-e^{-x}}{2}$

现在我们推导出等式的两边：

$\displaystyle\bigl(\text{senh}(x)\bigr)'=\left(\frac{e^x-e^{-x}}{2}\right)'$

为了导出方程的右侧，我们将使用除法导数的公式：

$\displaystyle\text{senh}'(x)=\frac{(e^x+e^{-x})\cdot 2}{2^2}=\frac{e^x+e^{-x}}{2}$

➤请参阅：以 e 为底的指数函数的导数

准确地说，我们已经得到了定义双曲余弦的表达式。从而证明双曲正弦的导数：

$\displaystyle\text{senh}'(x)=\text{cosh}(x)$

云奕文章网