本发明属于电力架空导线找形技术领域,具体涉及一种基于abaqus有限元软件的架空导线找形方法。
背景技术:
对于输电线路安全,分析它的各种受力状况是研究线路安全的基础。输电线作为一种悬索结构,只能受拉而不能受压,而且不承受弯矩,导线的初始构型关系在导线在动力学分析中有着重要地位,确定导线的初始构型是分析导线动力学响应的起点,直接关系到了以后的计算精度。
目前基于有限元软件的找形方法有以下几种:
1、直接迭代法,该方法见于张旺海的“基于ansys的架空输电导线找形研究”以及李力的“基于ansys的输电导线找形方法研究”;
2、小弹性模量法,该方法见于张旺海的“基于ansys的架空输电导线找形研究”;
3、预制模型更新法:此方法见于孔伟的“架空输电线路导线在ansys中的找形分析”以及黄新波的“均匀覆冰下的架空线有限元找形分析”。
其中,直接迭代法和小弹性模量迭代法都有着连贯性差的缺点,小弹性模量法还需要设置外置循环,从而不断的更新模型,可操作性较差,预制模型更新法使用有局限性,不能对应更加复杂的情况,而且计算精度不高。
技术实现要素:
有鉴于此,本发明提供一种基于abaqus有限元软件的架空导线找形方法,以解决现有技术的不足。
本发明的技术方案是:
一种基于abaqus有限元软件的架空导线找形方法,包括以下步骤:
s1、计算重力作用下的导线长度和导线伸长量,求取无应力情况下导线长度即导线原长;
s2、计算导线挂点直线距离,将导线挂点直线距离和s1中计算得到的导线原长的大小作对比,从而判定导线的初始形状;
s3、按照导线的初始形状建模并预设初始装配应力,设置分析步中的衰减系数后进行有限元分析求取解算结果,获得模拟弧垂和模拟最大应力;
s4、计算解算结果的相对误差值并判定建模的正确性,若误差值符合预定阈值条件,结束解算,若误差值不符合预定阈值条件,返回s3校正分析步中的衰减系数后继续执行,直到符合预定阈值条件。
优选的,s1中计算重力作用下的导线长度和导线伸长量,求取无应力情况下导线长度的方法包括以下步骤:
s11、利用公式(1)计算所需参数h0
其中,h0为由导线属性确定的悬链线方程参数,无物理意义,σ0为导线重力下水平应力,a为导线的横截面积,p为导线单位长度质量,g为重力加速度;
s12、利用公式(2)计算曲线左端点的横坐标la
其中,la为导线左端点的横坐标,h0为悬链线方程参数,l为导线挂点水平距离,即档距,h为导线挂点竖直距离,即高差;
s13、利用公式(3)计算曲线右端点横坐标lb
lb=l+la(3)
其中,lb导线右端点横坐标;
s14、利用公式(4)计算重力作用下导线长度l
其中,l为重力作用下导线长度;
s15、利用公式(5)计算重力作用下的导线伸长量δl
其中,δl为重力引起的导线伸长量,e为弹性模量;
s16、利用公式(6)计算无应力情况下导线长度l0
l0=l-δl(6)
其中,l0为无应力情况下导线长度即导线原长,δl为重力引起的导线伸长量,l为重力作用下导线长度。
优选的,所述s2中判定导线的初始形状的方法包括以下步骤:
s21、利用公式(7)计算导线挂点直线距离ls
其中,ls为导线挂点直线距离,l为导线挂点水平距离,即档距,h为导线挂点竖直距离,即高差;
s22、利用公式(8)计算无应力情况下导线长度l0和导线挂点直线距离ls之间的差值c
c=l0-ls(8)
其中,c为无应力情况下导线长度l0和导线挂点直线距离ls之间的差值,ls为导线挂点直线距离,l0为无应力情况下导线长度,即导线原长;
s23、判定导线的初始形状,判定方法是:
若c≤0,导线的初始形状为直线,
若c>0,导线的初始形状为v形折线。
优选的,所述s4中计算解算结果的相对误差值并判定建模的正确性的方法包括以下步骤:
s41、利用公式(9)计算导线弧垂处横坐标xmid
其中,xmid为导线弧垂处横坐标,h0为悬链线方程参数,h为导线挂点竖直距离,即高差,l为导线挂点水平距离,即档距;
s42、利用公式(10)计算理论弧垂f
其中,f为理论弧垂,la为导线左端点横坐标,lb导线右端点横坐标;
s43、利用公式(11)计算理论最大应力σmax
其中,σmax为理论最大应力,m取la和lb中绝对值较大的数,h0为悬链线方程参数,a为导线的横截面积,p为导线单位长度质量,g为重力加速度;
s44、利用公式(12)计算导线弧垂相对误差δ1
其中,δ1为导线弧垂相对误差,f1为模拟弧垂,f为理论弧垂;
s45、利用公式(13)计算导线最大应力相对误差δ2
其中,δ2为导线最大应力相对误差,σmax1为模拟最大应力,σmax为理论最大应力;
s46、设定预定阈值为5%,若δ1≤5%且δ2≤5%,则建模条件正确,符合预定阈值条件,模拟成功;若δ1>5%或δ2>5%,则相对误差值不符合预定阈值条件。
与现有技术相比,本发明提供的一种基于abaqus有限元软件的架空导线找形方法操作简单,可操作性好,计算结果稳定,精确度高,实用性好,值得推广。
附图说明
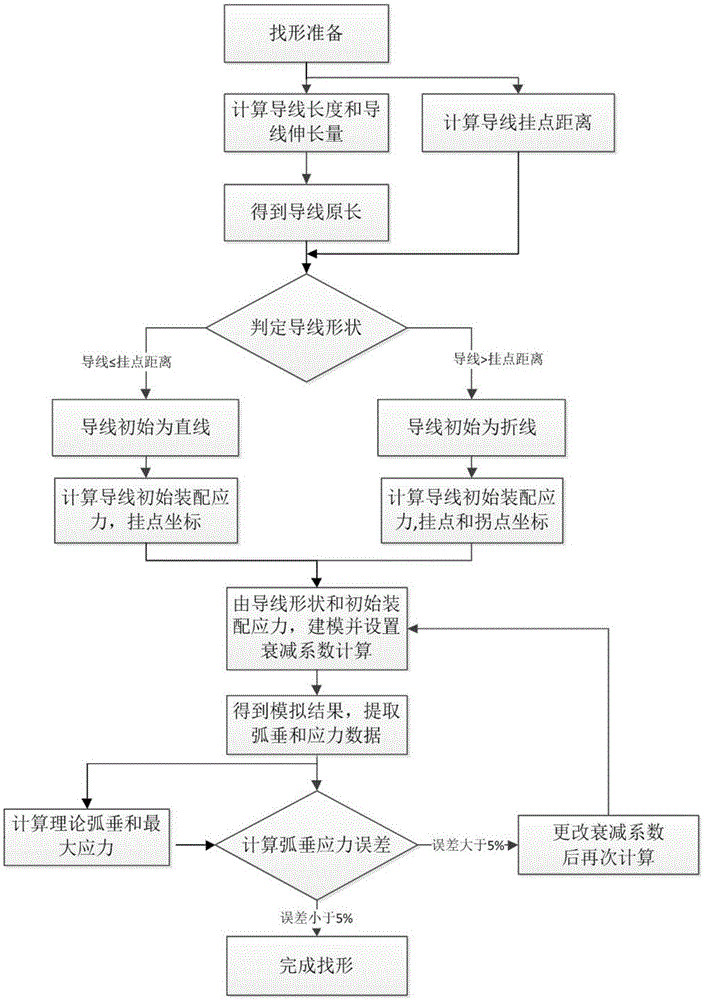
图1为本发明的找形方法的流程示意图;
图2为本发明的导线带塔示意图;
图3为本发明满足导线拐点坐标条件的椭圆。
具体实施方式
本发明提供了一种基于abaqus有限元软件的架空导线找形方法,下面结合图1到图3,对本发明进行说明。
如图1所示,本发明提供的一种基于abaqus有限元软件的架空导线找形方法,包括以下步骤:
s1、计算重力作用下的导线长度和导线伸长量,求取无应力情况下导线长度即导线原长;
s2、计算导线挂点直线距离,将导线挂点直线距离和s1中计算得到的导线原长的大小作对比,从而判定导线的初始形状;
s3、按照导线的初始形状建模并预设初始装配应力,设置分析步中的衰减系数后进行有限元分析求取解算结果,获得模拟弧垂和模拟最大应力;
s4、计算解算结果的相对误差值并判定建模的正确性,若误差值符合预定阈值条件,结束解算,若误差值不符合预定阈值条件,返回s3校正分析步中的衰减系数后继续执行,直到符合预定阈值条件。
进一步的,s1中计算重力作用下的导线长度和导线伸长量,求取无应力情况下导线长度的方法包括以下步骤:
s11、利用公式(1)计算所需参数h0
其中,h0为由导线属性确定的悬链线方程参数,无物理意义,σ0为导线重力下水平应力,a为导线的横截面积,p为导线单位长度质量,g为重力加速度;
s12、利用公式(2)计算曲线左端点的横坐标la
其中,la为导线左端点的横坐标,h0为悬链线方程参数,l为导线挂点水平距离,即档距,h为导线挂点竖直距离,即高差;
s13、利用公式(3)计算曲线右端点横坐标lb
lb=l+la(3)
其中,lb导线右端点横坐标;
s14、利用公式(4)计算重力作用下导线长度l
其中,l为重力作用下导线长度;
s15、利用公式(5)计算重力作用下的导线伸长量δl
其中,δl为重力引起的导线伸长量,e为弹性模量;
s16、利用公式(6)计算无应力情况下导线长度l0
l0=l-δl(6)
其中,l0为无应力情况下导线长度即导线原长,δl为重力引起的导线伸长量,l为重力作用下导线长度。
进一步的,所述s2中判定导线的初始形状的方法包括以下步骤:
s21、利用公式(7)计算导线挂点直线距离ls
其中,ls为导线挂点直线距离,l为导线挂点水平距离,即档距,h为导线挂点竖直距离,即高差;
s22、利用公式(8)计算无应力情况下导线长度l0和导线挂点直线距离ls之间的差值c
c=l0-ls(8)
其中,c为无应力情况下导线长度l0和导线挂点直线距离ls之间的差值,ls为导线挂点直线距离,l0为无应力情况下导线长度,即导线原长;
s23、判定导线的初始形状,判定方法是:
若c≤0,导线的初始形状为直线,
若c>0,导线的初始形状为v形折线。
进一步的,s4中计算解算结果的相对误差值并判定建模的正确性的方法包括以下步骤:
s41、利用公式(9)计算导线弧垂处横坐标xmid
其中,xmid为导线弧垂处横坐标,h0为悬链线方程参数,h为导线挂点竖直距离,即高差,l为导线挂点水平距离,即档距;
s42、利用公式(10)计算理论弧垂f
其中,f为理论弧垂,la为导线左端点横坐标,lb导线右端点横坐标;
s43、利用公式(11)计算理论最大应力σmax
其中,σmax为理论最大应力,m取la和lb中绝对值较大的数,h0为悬链线方程参数,a为导线的横截面积,p为导线单位长度质量,g为重力加速度;
s44、利用公式(12)计算导线弧垂相对误差δ1
其中,δ1为导线弧垂相对误差,f1为模拟弧垂,f为理论弧垂;
s45、利用公式(13)计算导线最大应力相对误差δ2
其中,δ2为导线最大应力相对误差,σmax1为模拟最大应力,σmax为理论最大应力;
s46、设定预定阈值为5%,若δ1≤5%且δ2≤5%,则建模条件正确,符合预定阈值条件,模拟成功;若δ1>5%或δ2>5%,则相对误差值不符合预定阈值条件。
其中,当导线初始形状为直线时,在abaqus中有限元建模仿真的方法包括以下步骤:
(1)计算导线挂点坐标
取导线挂点连线中点为原点,则左挂点为右挂点为
(2)利用公式(14)计算建模所需导线初始装配应力σl
其中,σl为导线初始装配应力;
(3)进入有限元软件进行建模,在软件中以两挂点b1,b2直接建立直线;
(4)模型施加约束:
在初始分析步中,将建好的导线模型两端简支,即固定两端x,y,z三个个方向的位移;
(5)模型施加重力:在随后的分析步中,在模型中施加重力加速度g,
设置衰减系数,使用系统的默认值即可;
(6)划分网格后,提交并进行计算。
其中,当导线初始形状为v形时,在abaqus中有限元建模仿真的方法包括以下步骤:
(1)计算导线挂点坐标以及导线拐点坐标;
取导线挂点连线中点为原点,则左挂点为右挂点为
需计算拐点坐标,拐点q(x1,y1)满足以下公式(15),见图3:
利用公式(16)计算当拐点位于中间位置时的坐标点d(x2,y2)
其中,为导线左挂点坐标,为导线右挂点坐标,q(x1,y1)为折线拐点一般情况下的坐标,d(x2,y2)为折线拐点中间位置时的坐标。
(2)得到初始装配应力
这里导线初始装配应力为零,但是为了有限元软件运算的收敛这里需要使导线处于紧绷,所以设置σl=1000mpa,小于应力mpa级别的1%,对结果影响不大。
(3)进入有限元软件进行建模,在软件中以两挂点b1,b2和拐点d建立折线。
(4)模型施加约束:在初始分析步中,将建好的导线模型两端简支,即固定两端x,y,z三个方向的位移。
(5)模型施加重力:在随后的分析步中,在模型中施加重力加速度g,设置衰减系数,使用默认即可。
(6)划分网格后,提交并进行计算。
其中,建模完成后,在软件的后处理结果中即可获取模拟弧垂f1和模拟最大应力σmax1。
本发明的找形方法首先根据设定的导线最低点水平应力得到无应力情况下导线长度,然后利用有限元软件进行非线性有限元分析完成导线的找形,计算不考虑重力作用时的导线初始长度是本方法的关键之处。
计算原理:
导线为不可压缩且不可承受弯矩的索,导线形状为悬链线,曲线为平面曲线,简化为平面问题。
根据悬链线的相关方程,可以求得导线在受重力作用下的导线弧长,以及导线各点应力的理论值。
根据导线各点应力值计算得到重力引起的导线伸长量,而无应力情况下导线长度是受重力作用下的导线长度与重力引起的导线伸长量之差,利用无应力情况下导线长度,导线挂点距离以及胡克定律可得导线初始装配应力,进而得到导线初始形状。
在有限元软件中根据导线初始形状建模,并施加初始装配应力,然后施加重力进行计算,就可以得到导线在重力下的初始构型。
实施例1:
如图2所示,现有一导线模型,其具体数据为,弹性模量e=55gpa,直径26.81mm,横截面积为426.28mm2,自重为1.18kg/m,现将其安装在档距为300m,无高差的两座塔之间,安装时水平应力为30mpa,分析并计算导线的形状以及内力。
详细过程:
计算所需参数
其中,h0为由导线属性确定的悬链线方程参数,σ0为导线重力下水平应力,
a为导线的横截面积,p为导线单位长度的质量,g为重力加速度;
计算曲线左端点,右端点
lb=l+la=150
其中,la为导线左端点横坐标,lb为导线右端点横坐标;l为导线档距,h为导线高差。
计算重力作用下导线长度
其中,l为重力作用下导线长度;
计算重力引起的导线伸长量
其中,δl为重力引起的导线伸长量,e为弹性模量;
计算导线初始形状和初始装配应力:
其中,l0为无应力情况下导线长度,即导线原长,ls为导线挂点的直线距离,c为导线长度和导线挂点直线距离之间的差值。
这里c>0,设σl=1000mpa,导线的初始形状为v形折线,
计算拐点坐标
其中,σl为导线无重力情况下的导线内的应力,d(x2,y2)为折线拐点中间位置时的坐标。
在abaqus软件中建模,将模型两端简支,导线上施加预应力重力,然后模拟计算,求取解算结果后得到模拟弧垂f1=10.1899m,模拟最大应力σmax1=30.25mpa。
理论计算:f=10.1885m,σmax=30.276mpa。
计算相对误差值:
其中,δ1为导线弧垂相对误差,δ2为导线最大应力相对误差,f1为模拟弧垂,σmax1为模拟最大应力,f为理论弧垂,σmax为理论导线最大应力。
误差满足阈值条件,模拟成功。
实施例2:
现有一导线模型,其具体数据为,弹性模量e=55gpa,直径26.81mm,横截面积为426.28mm2,自重为1.18kg/m,现将其安装在档距为300m,高差为50m的两座塔之间,安装时水平应力为55.1mpa,分析并计算导线的形状以及内力。
详细过程:
计算所需参数
其中,h0为由导线属性确定的悬链线方程参数,σ0为导线重力下水平应力,a为导线的横截面积,p为导线单位长度的质量,g为重力加速度;
计算曲线左端点,右端点
lb=l+la=-186.6710
其中,la为导线左端点横坐标,lb为导线右端点横坐标,l为导线档距,h为导线高差。
计算重力作用下导线长度
其中,l为重力作用下导线长度;
计算重力引起的导线伸长量
其中,δl为由重力引起的导线伸长量,e为弹性模量,
计算导线初始构型和初始装配应力:
其中,l0为导线无重力情况下的长度,ls为导线挂点的直线距离,c为导线长度和导线挂点直线距离之间的差值。
这里c0,设σl=1000mpa,导线的初始形状为v形折线,
计算过程中,为了验证拐点的选取可以取任意点,如图3所示的满足导线拐点坐标条件的椭圆,这里设置拐点为1/3处,令x1=100,带入椭圆方程得到y1=-10.0649,其中σl为导线无重力情况下导线内的应力,(x1,y1)为折线拐点为1/4处时的坐标,其中f为导线和挂点连线的最大值,即弧垂;
在abaqus软件中建模,将模型两端简支,导线上施加预应力,然后模拟计算得到结果,模拟弧垂f1=10.186m,模拟最大应力σmax1=30.28mpa。
理论值:f=10.1885m,σmax=30.276mpa。
计算相对误差值:
其中,δ1为导线弧垂相对误差,δ2为导线最大应力相对误差,f1为模拟弧垂,σmax1为模拟最大应力,f为理论弧垂,σmax为理论导线最大应力。
误差满足,模拟成功。
与现有技术相比,本发明提供的一种基于abaqus有限元软件的架空导线找形方法,建模简单,减少了计算步骤,减轻了操作负担,计算结果稳定,能够收敛,适用范围广,实用性好,值得推广。
以上公开的仅为本发明的较佳的具体实施例,但是,本发明实施例并非局限于此,任何本领域技术人员能思之的变化都应落入本发明的保护范围。