(1)首先求得导函数的解析式，然后分类讨论即可确定函数的单调性；

(2)将原问题进行等价转化，然后构造新函数，利用导函数研究函数性质并进行放缩即可确定实数a的取值范围；

(3)结合(2)的结论将原问题进行等价变形，然后利用分析法即可证得题中的结论成立.

【详解】(1)，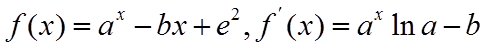

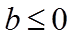
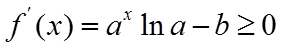
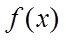
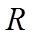
①若，则，所以在上单调递增；

②若，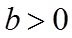

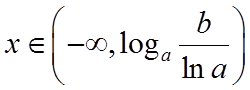
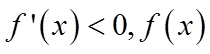
当时，单调递减，

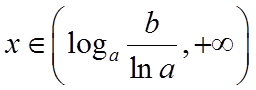
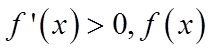
当时，单调递增.

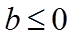
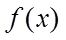
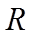
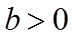
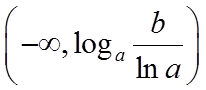
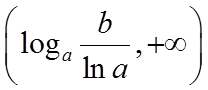
综上可得，时，在上单调递增；

时，函数的单调减区间为，单调增区间为.

(2)有2个不同零点有2个不同解有2个不同的解，

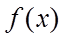
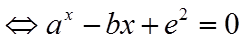
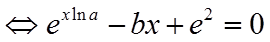
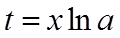
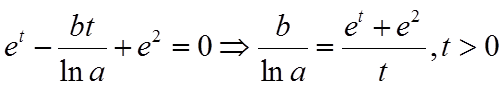
令，则，

记，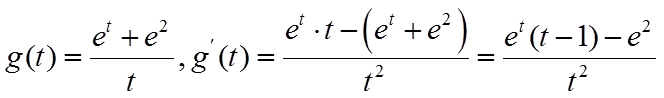

记，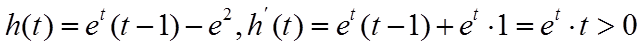

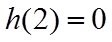
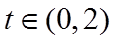
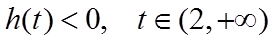
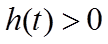
又，所以时，时，，

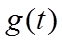
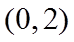
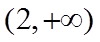
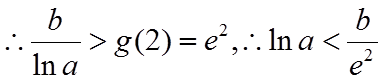
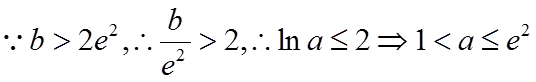
则在单调递减，单调递增，，

.

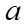
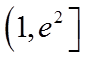
即实数的取值范围是.

(3)有2个不同零点，则，故函数的零点一定为正数.

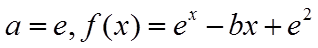
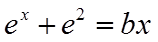
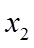
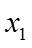
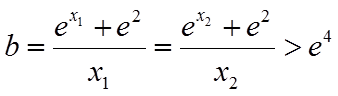
由(2)可知有2个不同零点，记较大者为，较小者为，

，

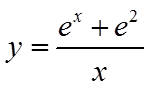
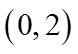
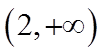
注意到函数在区间上单调递减，在区间上单调递增，

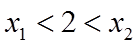
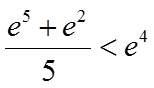
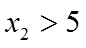
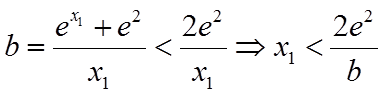
故，又由知，

，

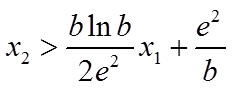
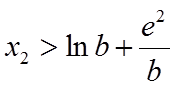
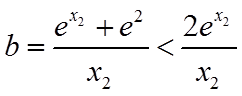
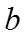
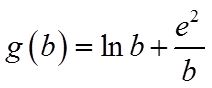
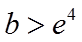
要证，只需，

且关于的函数在上单调递增，

所以只需证，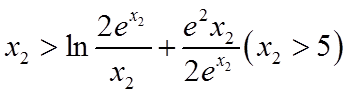

只需证，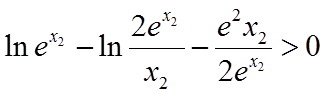

只需证，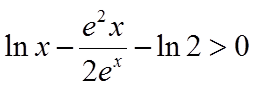

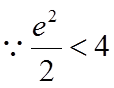
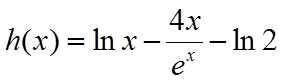
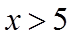
，只需证在时为正，

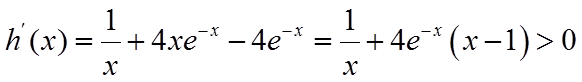
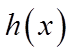
由于，故函数单调递增，

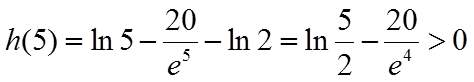
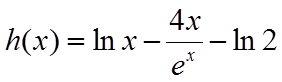
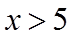
又，故在时为正，

从而题中的不等式得证.

【点睛】导数是研究函数的单调性、极值(最值)最有效的工具，而函数是高中数学中重要的知识点，所以在历届高考中，对导数的应用的考查都非常突出，从高考来看，对导数的应用的考查主要从以下几个角度进行：(1)考查导数的几何意义，往往与解析几何、微积分相联系．(2)利用导数求函数的单调区间，判断单调性；已知单调性，求参数．(3)利用导数求函数的最值(极值)，解决生活中的优化问题．(4)考查数形结合思想的应用．