这个例题可能是分析中你遇到的第一个BOSS，如果本例的证明你能看懂，那么恭喜你，你的分析已经达到了一个较高的段位。如果不能理解证明中戴尔他的取法，请按部就班地认真学习，也请关注大表哥的复习指南更新，我在本章对应的视频中会有详细的讲解，而且保证每个人都能打通任督二脉，冲破玄关！

马克思告诉我们，万事万物都是对立统一的，有连续的地方就一定有不连续！是的，老马识途，他错不了！有图有真相！

由此也有了间断点的分类：第一类间断点和第二类间断点！

间断点的考察，对于数学专业来说并不重要（公共数学考研一般出一个4分的选择题），因为间断的性质并不“好”。就像你考研一样，复习三五天，间断了。努力一个周，间断了。坚持了一个月，间断了！那还考个球球！

我们需要大量的连续函数，因为连续函数在某点连续时，具有局部有界性，局部保号性，四则运算法则和复合的性质。这些性质都很容易证明，而且几乎和函数极限存在的证明雷同。

函数在闭区间上连续，那性质就更“好”了！

闭区间上连续函数的四大性质，即有界性，最值性，介值性，一致连续性，是考研分析亘古不变的重点！请认真对待！

大表哥强烈建议同学们把教材上出现的有界性的引理，当成定理！

介值性定理有一个常考的推论，称为零点定理或根的存在性定理，

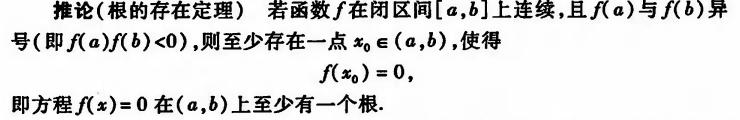
以上五个结论本身的证明，都有一定的难度，尤其介值性定理的证明（这个定理也可以当成检测分析段位的一个标准）。

而考研数学分析至少考查上述五个结论中的某个，尤其是其应用（也有很多学校考过结论本身的证明！比如西北大学，陕西师范大学就分别考过有界性和最值性的证明）！

上述五个结论，没有最重要，只有更重要！

大表哥特别要强调的是，最最重要的一致连续性！

一致连续是连续函数的一个整体性质，即：自变量两点之间的距离离得很近时，因变量之间的距离就不能离得太远。自变量的变化和因变量的变化保持一致，没有出现大起大落跌宕起伏一波三折的传奇人生，而是兢兢业业认认真真日复一日，最终肯定会一步一步稳稳当当如愿以偿地迎娶美富白，当上CEO，走上人生巅峰（算了，你还是努力攻读理学博士吧）。

定义一般可以解决一个具体函数的一致连续问题，比如证明线性函数的一致连续性，

大表哥的三个英文标题，你一定看的一头雾水，哇哈哈哈，那就对了，这叫信息加密！关注我的视频哟，会有详细说明！

图中例10给出的是个等价的刻画，往往也可以用它证明不一致连续！

而图中例12，以及本节课后的第14题，都是充分条件！

一致连续性的考察，很多院校都会考一个大题！请同学们在复习的时候，给与高度重视并且高度自练！

本章的第三节——初等函数的连续性，同学们不用深究，只需要记住两个常识性的结论即可：

至于本章的课后练习，还是和之前的要求一样，请努力独立地去完成横线上面的题目，有难度的题目可留到暑假强化阶段。

咱们第五章见！

我是大表哥，关注我，数学考研不翻车！

每周三晚19:30，B站直播，搜索“大表哥考研数学”或房间号：22089437，带你征服数学分析各章节重点难点！返回搜狐，查看