(1) lim x → 0 sin xx =1\lim _{x \rightarrow 0} \frac{\sin x}{x}=1limx→0xsinx=1, 推广形式 lim f ( x ) → 0 sin f ( x ) f ( x )=1\lim _{f(x) \rightarrow 0} \frac{\sin f(x)}{f(x)}=1limf(x)→0f(x)sinf(x)=1. (2) lim x → ∞ ( 1 +1x )x =e\lim _{x \rightarrow \infty}\left(1+\frac{1}{x}\right)^x=\mathrm{e}limx→∞(1+x1)x=e, 推广形式 lim x → 0(1+x)1 x=e, lim f ( x ) → ∞ [ 1 +1f(x) ] f ( x )=e\lim _{x \rightarrow 0}(1+x)^{\frac{1}{x}}=\mathrm{e}, \lim _{f(x) \rightarrow \infty}\left[1+\frac{1}{f(x)}\right]^{f(x)}=\mathrm{e}limx→0(1+x)x1=e,limf(x)→∞[1+f(x)1]f(x)=e
2. 常用的等价无穷小量及极限公式(1) 当x→0x \rightarrow 0x→0 时,常用的等价无穷小
(1) x ∼ sin x ∼ tan x ∼ arcsin x ∼ arctan x ∼ ln ( 1 + x ) ∼e x− 1 x \sim \sin x \sim \tan x \sim \arcsin x \sim \arctan x \sim \ln (1+x) \sim \mathrm{e}^x-1x∼sinx∼tanx∼arcsinx∼arctanx∼ln(1+x)∼ex−1.(2) 1 − cos x ∼1 2 x 2, 1 − cos bx ∼b 2 x 2( b ≠ 0 ) 1-\cos x \sim \frac{1}{2} x^2, 1-\cos ^b x \sim \frac{b}{2} x^2(b \neq 0)1−cosx∼21x2,1−cosbx∼2bx2(b=0).(3)a x− 1 ∼ x ln a ( a > 0 a^x-1 \sim x \ln a(a>0ax−1∼xlna(a>0, 且 a ≠ 1 ) a \neq 1)a=1).(4) ( 1 + x) α− 1 ∼ α x ( α ≠ 0 ) (1+x)^\alpha-1 \sim \alpha x (\alpha \neq 0)(1+x)α−1∼αx(α=0).(2) 当n→∞n \rightarrow \inftyn→∞ 或x→∞x \rightarrow \inftyx→∞ 时,常用的极限公式
(1) limn→∞ n n= 1 , limn→∞ a n= 1 ( a > 0 ) \lim _{n \rightarrow \infty} \sqrt[n]{n}=1, \lim _{n \rightarrow \infty} \sqrt[n]{a}=1(a>0)limn→∞nn =1,limn→∞na =1(a>0).(2) limx→∞anxn+an − 1 xn − 1 +⋯+a1x+a0bmxm+bm − 1 xm − 1 +⋯+b1x+b0={a n b m ,n=m,0,n为 0 .
(3) limn→∞ x n={0,∣x∣<1,∞,∣x∣>1,1,x=1, 不存在, x=−1;limn→∞enx ={0,x<0,+∞,x>0,1,x=0.\lim _{n \rightarrow \infty} x^n=\left\{\begin{array}{ll}0, & |x|1, \\ 1, & x=1, \\ \text { 不存在, } & x=-1 ;\end{array} \lim _{n \rightarrow \infty} \mathrm{e}^{n x}= \begin{cases}0, & x0, \\ 1, & x=0 .\end{cases}\right.limn→∞xn=⎩⎪⎪⎨⎪⎪⎧0,∞,1, 不存在, ∣x∣1,x=1,x=−1;limn→∞enx=⎩⎪⎨⎪⎧0,+∞,1,x0,x=0.(4) 若 lim g ( x ) = 0 , lim f ( x ) = ∞ \lim g(x)=0, \lim f(x)=\inftylimg(x)=0,limf(x)=∞, 且 lim g ( x ) f ( x ) = A \lim g(x) f(x)=Alimg(x)f(x)=A, 则有 lim [ 1 + g ( x )]f(x) =eA .\lim [1+g(x)]^{f(x)}=\mathrm{e}^A . lim[1+g(x)]f(x)=eA. 3.x→0x \rightarrow 0x→0 时常见的麦克劳林公式sin x = x −13! x 3+ o(x3 ),cos x = 1 −12! x 2+14! x 4+ o(x4 ),tan x = x +1 3 x 3+ o(x3 ),arcsin x = x +13! x 3+ o(x3 ),arctan x = x −1 3 x 3+ o(x3 ),ln ( 1 + x ) = x −1 2 x 2+1 3 x 3+ o(x3 ), e x= 1 + x +12! x 2+13! x 3+ o(x3 ), ( 1 + x) a= 1 + a x + a(a−1)2! x 2+ o(x2 ). \begin{aligned} & \sin x=x-\frac{1}{3 !} x^3+o\left(x^3\right), \quad \cos x=1-\frac{1}{2 !} x^2+\frac{1}{4 !} x^4+o\left(x^4\right),\\ \\ & \tan x=x+\frac{1}{3} x^3+o\left(x^3\right), \quad \arcsin x=x+\frac{1}{3 !} x^3+o\left(x^3\right), \\ \\ & \arctan x=x-\frac{1}{3} x^3+o\left(x^3\right), \quad \ln (1+x)=x-\frac{1}{2} x^2+\frac{1}{3} x^3+o\left(x^3\right), \\ \\ & \mathrm{e}^x=1+x+\frac{1}{2 !} x^2+\frac{1}{3 !} x^3+o\left(x^3\right),(1+x)^a=1+a x+\frac{a(a-1)}{2 !} x^2+o\left(x^2\right) . \end{aligned}sinx=x−3!1x3+o(x3),cosx=1−2!1x2+4!1x4+o(x4),tanx=x+31x3+o(x3),arcsinx=x+3!1x3+o(x3),arctanx=x−31x3+o(x3),ln(1+x)=x−21x2+31x3+o(x3),ex=1+x+2!1x2+3!1x3+o(x3),(1+x)a=1+ax+2!a(a−1)x2+o(x2).
当x→0x \rightarrow 0x→0 时,由以上公式可以得到以下几组“差函数”的等价无穷小代换式:
x−sinx∼ x 36 ,tanx−x∼ x 33 ,x−ln(1+x)∼ x 22 x-\sin x \sim \frac{x^3}{6}, \quad \tan x-x \sim \frac{x^3}{3}, \quad x-\ln (1+x) \sim \frac{x^2}{2}x−sinx∼6x3,tanx−x∼3x3,x−ln(1+x)∼2x2,arcsinx−x∼ x 36 ,x−arctanx∼ x 33 \arcsin x-x \sim \frac{x^3}{6}, \quad x-\arctan x \sim \frac{x^3}{3}arcsinx−x∼6x3,x−arctanx∼3x3.
4. 基本导数公式 (xμ) ′= μxμ−1( μ 为 常 数 ) , (ax) ′=a xln a ( a > 0 , a ≠ 1 ) , (log ax) ′=1xlna( a > 0 , a ≠ 1 ) , ( ln x) ′=1 x, ( sin x) ′= cos x , ( cos x) ′= − sin x , ( arcsin x) ′=11−x 2 , ( arccos x) ′= −11−x 2 , ( tan x) ′= sec 2x , ( cot x) ′= − csc 2x , ( arctan x) ′=11+x2, ( arccot x) ′= −11+x2, ( sec x) ′= sec x tan x , ( csc x) ′= − csc x cot x , [ln( x + x2+1) ]′ =1 x 2+ 1,, [ln(x+x2 − 1)] ′=1x 2 −1\begin{array}{ll} \left(x^\mu\right)^{\prime}=\mu x^{\mu-1} ( \mu 为常数), & \left(a^x\right)^{\prime}=a^x \ln a(a>0, a \neq 1), \\ \\ \left(\log _a x\right)^{\prime}=\frac{1}{x \ln a}(a>0, a \neq 1) , & (\ln x)^{\prime}=\frac{1}{x}, \\ \\ (\sin x)^{\prime}=\cos x, & (\cos x)^{\prime}=-\sin x, \\ \\ (\arcsin x)^{\prime}=\frac{1}{\sqrt{1-x^2}}, & (\arccos x)^{\prime}=-\frac{1}{\sqrt{1-x^2}}, \\ \\ (\tan x)^{\prime}=\sec ^2 x, & (\cot x)^{\prime}=-\csc ^2 x, \\ \\ (\arctan x)^{\prime}=\frac{1}{1+x^2}, & (\operatorname{arccot} x)^{\prime}=-\frac{1}{1+x^2}, \\ \\ (\sec x)^{\prime}=\sec x \tan x, & (\csc x)^{\prime}=-\csc x \cot x, \\ \\ {\left[\ln \left(x+\sqrt{x^2+1}\right)\right]^{\prime}=\frac{1}{\sqrt{x^2+1}},}, & {\left[\ln \left(x+\sqrt{x^2-1}\right)\right]^{\prime}=\frac{1}{\sqrt{x^2-1}}} \end{array}(xμ)′=μxμ−1(μ为常数),(logax)′=xlna1(a>0,a=1),(sinx)′=cosx,(arcsinx)′=1−x2 1,(tanx)′=sec2x,(arctanx)′=1+x21,(secx)′=secxtanx,[ln(x+x2+1 )]′=x2+1 1,,(ax)′=axlna(a>0,a=1),(lnx)′=x1,(cosx)′=−sinx,(arccosx)′=−1−x2 1,(cotx)′=−csc2x,(arccotx)′=−1+x21,(cscx)′=−cscxcotx,[ln(x+x2−1 )]′=x2−1 1 三角函数六边形记忆法: 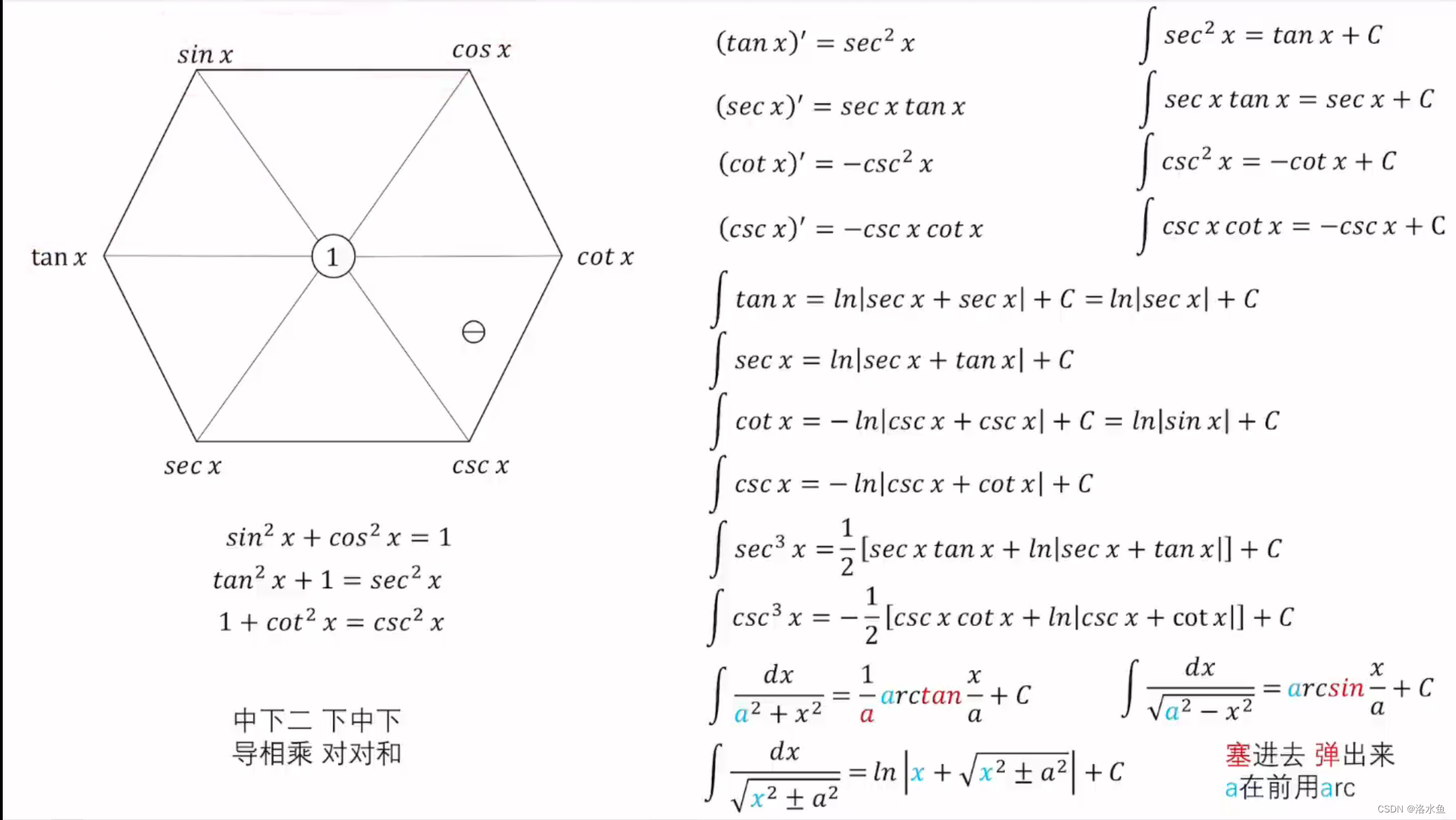
注: 变限积分求导公式. 设F(x)=∫ φ2 ( x )φ1 ( x )f(t)dtF(x)=\int_{\varphi_2(x)}^{\varphi_1(x)} f(t) \mathrm{d} tF(x)=∫φ2(x)φ1(x)f(t)dt, 其中f(x)f(x)f(x) 在[a,b][a, b][a,b] 上连续, 可导函数φ 1 (x)\varphi_1(x)φ1(x) 和φ 2 (x)\varphi_2(x)φ2(x) 的值域在[a,b][a, b][a,b] 上, 则在函数φ 1 (x)\varphi_1(x)φ1(x) 和φ 2 (x)\varphi_2(x)φ2(x) 的公共定义域上有:F ′( x ) =ddx [∫φ 1 (x)φ 2 (x) f ( t ) d t ]= f[φ2 ( x ) ] φ 2 ′( x ) − f[φ1 ( x ) ] φ 1 ′( x ) . F^{\prime}(x)=\frac{\mathrm{d}}{\mathrm{d} x}\left[\int_{\varphi_1(x)}^{\varphi_2(x)} f(t) \mathrm{d} t\right]=f\left[\varphi_2(x)\right] \varphi_2^{\prime}(x)-f\left[\varphi_1(x)\right] \varphi_1^{\prime}(x) .F′(x)=dxd[∫φ1(x)φ2(x)f(t)dt]=f[φ2(x)]φ2′(x)−f[φ1(x)]φ1′(x).
5. 几个重要函数的麦克劳林展开式(1)e x =1+x+12 !x 2 +⋯+1n !x n +o(x n) \mathrm{e}^x=1+x+\frac{1}{2 !} x^2+\cdots+\frac{1}{n !} x^n+o\left(x^n\right)ex=1+x+2!1x2+⋯+n!1xn+o(xn).
(2)sinx=x−13 !x 3 +⋯+(−1) n 1( 2 n + 1 ) !x2 n + 1+o(x2n+1) \sin x=x-\frac{1}{3 !} x^3+\cdots+(-1)^n \frac{1}{(2 n+1) !} x^{2 n+1}+o\left(x^{2 n+1}\right)sinx=x−3!1x3+⋯+(−1)n(2n+1)!1x2n+1+o(x2n+1).
(3)cosx=1−12 !x 2 +14 !x 4 −⋯+(−1) n 1( 2 n ) !x2 n+o(x2n) \cos x=1-\frac{1}{2 !} x^2+\frac{1}{4 !} x^4-\cdots+(-1)^n \frac{1}{(2 n) !} x^{2 n}+o\left(x^{2 n}\right)cosx=1−2!1x2+4!1x4−⋯+(−1)n(2n)!1x2n+o(x2n).
(4)11 − x=1+x+x 2 +⋯+x n +o(x n) ,∣x∣<1\frac{1}{1-x}=1+x+x^2+\cdots+x^n+o\left(x^n\right),|x|