Step2:代入点坐标:即 , ;
Step3:作差得出结论:(1)-(2)得: (作为公式记住,在小题中直接用。)
同理可推出其余三类方程的中点弦结论:
② 。
③ 。
④ 。
【题型1】:求值,利用结论求k或斜率乘积定值。

【答案】D
【解析】
【答案】B
【解析】
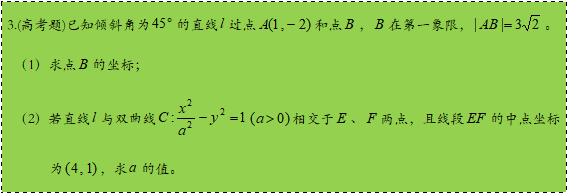
【解析】


【解析】
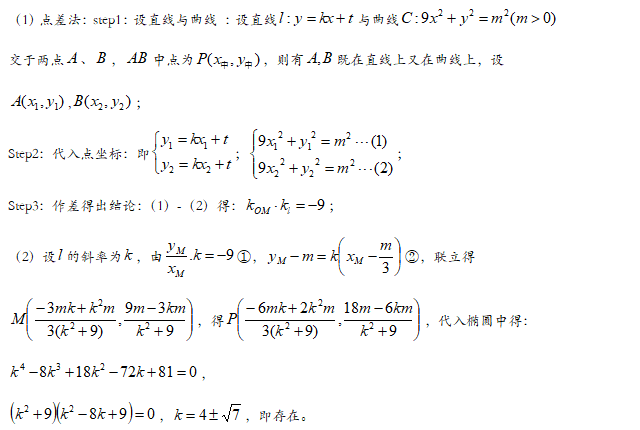

【解析】

结论:平行直线系,过椭圆中心(原点)时弦长最大。
【题型2】:求当 为定值时,平行弦中点轨迹。
法一:直线与曲线联立,利用根与系数的关系,求出中点坐标的参数方程,消参数即得中点弦轨迹方程。
法二:利用点差法得: ,即 (过原点的直线在曲线内部的部分)。

【解析】

【题型3】:求当直线 恒过一定点 时,得定点弦中点轨迹:利用 消去 。
法一:直线与曲线联立,利用根与系数的关系,求出中点坐标的参数方程,消参数即得中点弦轨迹方程。
法二:利用点差法得: ,即 。

【解析】

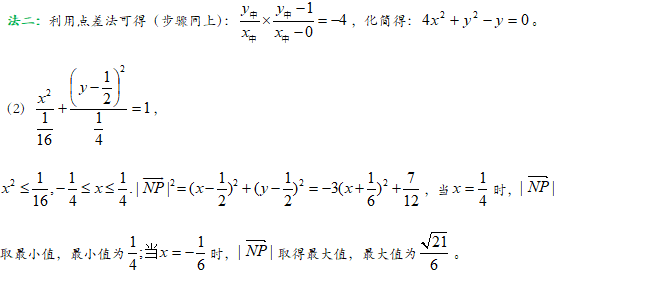
【技巧二】抛物线中点弦问题。
『秒杀策略』:抛物线:① 。
简答题步骤规范模板:
方法一:
①设直线 的方程;
②直线与曲线联立,整理成关于 (或 )的一元二次方程;
③写出根与系数的关系;
④利用 ,把根与系数的关系代入。
方法二:点差法:
step1:设直线 与曲线 : 交于两点 、 ,中点为 ,则有 既在直线上又在曲线上,设 ,
Step2:代入点坐标:即 , ;
Step3:作差得出结论:(1)-(2)得: (作为公式记住,在小题中直接用。)
同理可推出其余三类方程的中点弦结论:
② 。
③ 。
④ 。
【题型4】:求值(求k或p)。
【答案】
【解析】
【答案】B
【解析】
【答案】2
【解析】
【答案】
【解析】
圆锥曲线的双切线问题处理技巧
【方法点拨】
这类试题主要的点在算理,即计算中如何合理的处理双切线,我总结如下:已知曲线外一点 ,向二次曲线 引两条切线 ,设 .
第1步:分别写出切线的方程(注意斜率);
第2步:联立与曲线的方程,利用相切条件,得到代数关系①,②式,从而以的 或 坐标为参数,进一步构造点横或纵坐标满足的同构方程方程③;
第3步:利用方程③根与系数的关系判断与曲线的位置关系,或完成其他问题.
【典例赏析】
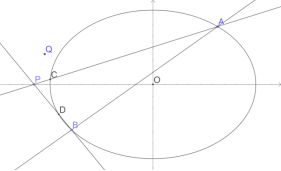
(2021甲卷)已知抛物线 的顶点为坐标原点 ,焦点在 轴上,直线 交 于 两点,且 .已知点 ,且⨀ 与 相切.
(1)求 ,⨀ 的方程;
(2)设 是 上的三个点,直线 均与⨀ 相切,判断直线 与⨀ 的位置关系,并说明理由.
【解析】
(1)设 的方程为 ,
由对称性可知, ,并假设点 在第一象限,点 在第四象限,
故直线 将代入抛物线方程解得: ,
又因为 ,故 ,即
代入点 坐标可得: ,
故 的方程为 .
再由直线 与⨀ 相切可得⨀ : .
(2)直线 与⨀ 相切.
理由如下:
假设直线的斜率都存在,设 ,
则可得 的方程为: ,整理可得: ,
由直线 与⨀ 相切得: ,整理得: ①
同理: 的方程为 ,
由 与⨀ 相切,即 ②.
由①,②可知 分别是下列方程的两根, ③.
若 ,代入③式得: ,
与是三个不重合的点矛盾,故 ,
则 , ④,
最后,由于 直线的方程为 ,
那么圆心 到直线 的距离为 ,
代入④式得: .
故直线 与⨀ 相切.
当直线的斜率有一条不存在时,根据⨀ 的位置关系可知,此时切线要么为 ,要么为 .
不妨假设当 切线为 时,那么此时切线 为 ,不合题意.
假设当 切线为 时,可取两点坐标为 ,
设切线 的方程为 ,其与⨀ 相切,故 ,得 .
即此时,切线 ,过坐标原点与⨀ 相切,即 .
这样: 的方程为: ,与 关于 轴对称,根据对称性可知 与⨀ 相切,综上所述,直线 与⨀ 相切.
变式1. (2020成都三诊).已知椭圆 : 的左焦点 ,点 在椭圆 上.
(1)求椭圆 的标准方程;
(2)经过圆 : 上一动点 作椭圆 的两条切线,切点分别记为 , ,直线 , 分别与圆 相交于异于点 的 , 两点.
(i)求证: ;
(ii)求 的面积的取值范围.
【解析】
(1)∵椭圆 的左焦点 ,
∴ .
将 代入 ,得 .
又 ,
∴ .
∴椭圆的标准方程为 .
(2)(i)设点 .
①当直线 , 的斜率都存在时,
设过点 与椭圆 相切的直线方程为 .
由 ,消去 ,
得 .
令 ,整理得 .
设直线 , 的斜率分别为
∴ .
又 ,∴ .
∴ ,即为圆 的直径,
∴ .
②当直线 或 的斜率不存在时,
不妨设 ,则直线 的方程为 .
∴ , ,也满足 .
综上,有 .
(ii)设点 .
当直线 的斜率存在时,设直线 的方程为 .
由 ,消去 ,
得
令 ,整理得 .
则
∴直线 的方程为 .
化简可得 ,即 .
经验证,当直线 的斜率不存在时,
直线 的方程为 或 ,也满足 .
同理,可得直线 的方程为 .
∵ 在直线 , 上,即 , .
∴直线 的方程为 .
由 ,消去 ,得 .
∴ , .
又点 到直线 的距离 .
∴ .
令 , .
则 .
又 ,
∴ 的面积的取值范围为 .
圆锥曲线选填压轴之距离
【方法点拨】
1.距离的几何意义:
(1)数轴上的距离: (终点减去起点的绝对值)
(2)平面内的距离: (构造直角三角形证明)
(3)三角形的边的关系:
2.距离的代数表达:
(1)点到点的距离公式:
(2)点到直接的距离公式: ,
(3)两条平行线的距离公式: .
【基本方法】
1.几何转化法:充分利用代数表达式转化为几何意义;
2.坐标转化法:充分利用点和线段的坐标化,将几何图形问题转化为坐标运算问题;
3.构造函数法:恰当引入参数,建立函数关系,求解与距离相关的最值问题.
【典例赏析】
类型一直接利用距离转化

【答案】A
【解析】
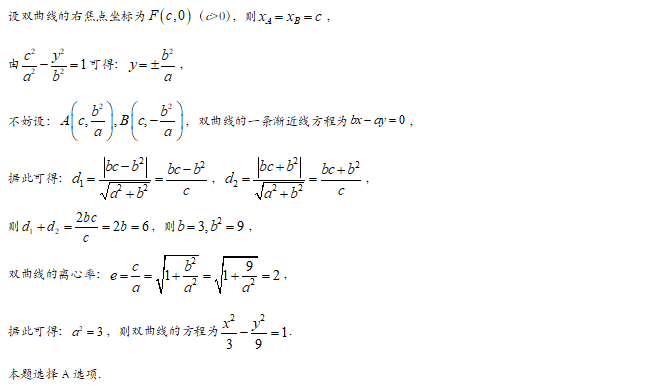
【答案】B
【解析】
【答案】A
【解析】
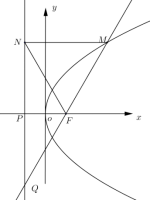
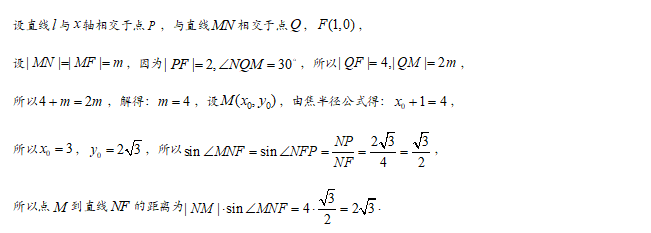
【答案】B
【解析】

【答案】A
【解析】

类型二将距离问题转化坐标运算
【答案】D
【解析】
【答案】B
【解析】

【答案】C
【解析】

【答案】B
【解析】
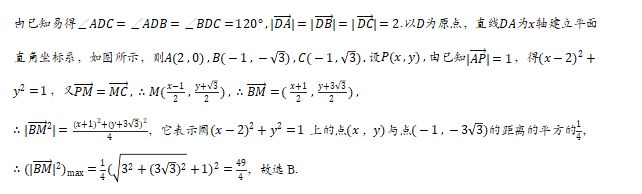
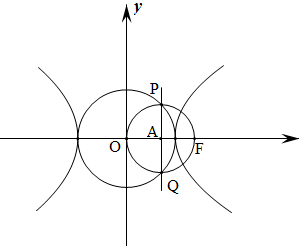
【答案】A
【解析】
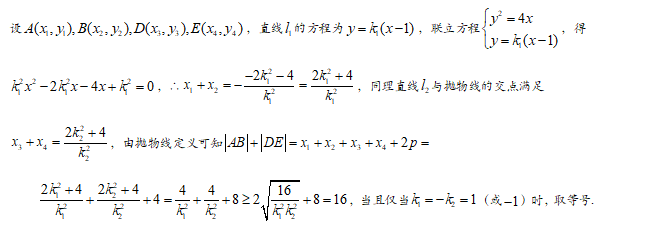
【答案】B
【解析】

三.利用距离的几何意义求解
【答案】A
【解析】
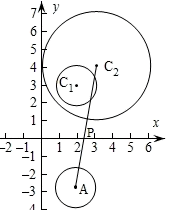
【答案】D
【解析】
【答案】B
【解析】
【答案】A
【解析】
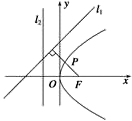

【答案】A
【解析】
【答案】B
【解析】
法一:
法二:

【答案】B
【解析】
圆锥曲线压轴题之切线问题
综述
圆锥曲线的切线问题有两种处理方法:
方法1:导数法,将圆锥曲线方程化为函数 ,利用导数法求出函数 在点 处的切线方程,特别是焦点在 轴上常用此法求切线;
方法2:根据题中条件设出切线方程,将切线方程代入圆锥切线方程,化为关于(或y)的一元二次方程,利用切线与圆锥曲线相切的充要条件为判别式 ,即可解出切线方程,注意关于 (或y)的一元二次方程的二次项系数不为0这一条件,圆锥曲线的切线问题要根据曲线不同,选择不同的方法
与切线有有关的结论:
1.椭圆的切线方程:椭圆 上一点 处的切线方程是 ;椭圆 外一点 所引两条切线的切点弦方程是 .
2.双曲线的切线方程:双曲线 ,上一点 处的切线方程是 ;双曲线 ,外一点 所引两条切线的切点弦方程是 .
3.抛物线的切线方程:抛物线 上一点处的切线方程是 ;抛物线 外一点 所引两条切线的切点弦方程是 .
4.设抛物线 的焦点为 ,若过点 的直线 分别与抛物线 相切于 两点,则 .
5.设椭圆的焦点为 ,若过点 的直线 分别与椭圆相切于 两点,则.
6.设双曲线,的焦点为 ,若过点 的直线 分别与双曲线相切于 两点,则.
【典例赏析】
(一)与圆有关的切线问题

【解析】



【解析】
(2)(i)本题有两种解法:
(方法一) :椭圆和圆有公切线时求点 的坐标,可先设公切线方程为
然后根据直线分别与圆和椭圆相切求出的 值,再求出点 的坐标,这个方法很容易想到,但是需要两次计算相切时的条件。
(方法二) :题目中让求点 的坐标,不如一开始就设出点 的坐标,利用点 的坐标表示出切线方程,然后直线与椭圆联立, 即可求出点 的坐标。
这里我们选用第二种方法:

(ii)分析:第二问由于 的高即为圆的半径,故由面积可以得出弦长 的值,根据弦长再求出直线方程,最容易想到的就是设出直线方程,根据直线与圆相切可得 ,然后直线与椭圆联立,根据韦达定理写出弦长公式,将 或 转化成一个,求出即可,但是计算过程很麻烦,下面给出同一个方法的两种不同解法:

注意此处,根据韦达定理得出的两根和与积的形式本来很复杂,如果利用上式还需要进行平方,再将 转化为 的形式计算起来相当复杂,因此我们要想办法避开平方,因此不如直接根据直线与椭圆联立的方程解出两根,再利用弦长公式,就可以避开平方的出现,解法也会简单一些。
(二)与椭圆有关的切线问题

【解析】
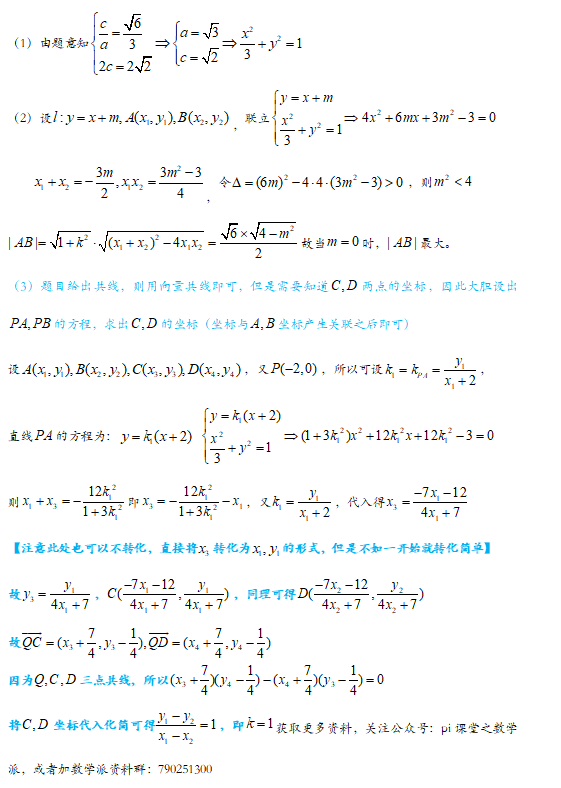
【答案】A
【解析】
(三)与抛物线有关的切线问题

【解析】

【答案】D
【解析】

【提高训练】(共7道题)
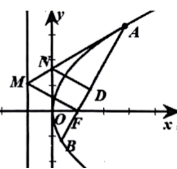
【答案】
【答案】
【答案】C
【解析】
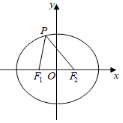
【答案】B
【解析】


【解析】
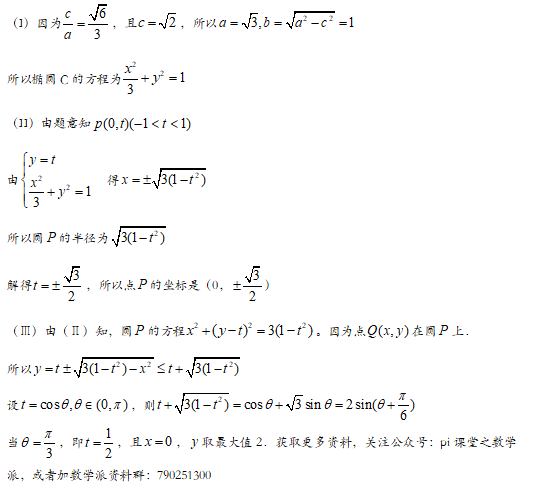

【解析】


【解析】

圆锥曲线选填压轴小题之面积问题
【基本知识】
1、弦长问题:设圆锥曲线 ∶ 与直线 相交于 , 两点,则弦长 为:
或 2、三角形面积问题:
直线 方程: ,
则 3.焦点三角形的面积:
直线 过焦点 , 的面积为
4.平行四边形的面积:
直线 方程: ,直线 方程: ,两直线之间的距离 ,则 5.面积的向量表示:
(1)在 中,设 , ,则 (2)
【基本技能】
1、面积问题的解决策略:
(1)求三角形的面积需要寻底找高,需要两条线段的长度,为了简化运算,通常优先选择能用坐标直接进行表示的底(或高)。
(2)面积的拆分:不规则的多边形的面积通常考虑拆分为多个三角形的面积和,对于三角形如果底和高不便于计算,则也可以考虑拆分成若干个易于计算的三角形.
(3)多个图形面积的关系的转化:关键词“求同存异”,寻找这些图形的底和高中是否存在“同底”或“等高”的特点,从而可将面积的关系转化为线段的关系,使得计算得以简化.
2、面积范围的解决策略:
通常利用公式将面积转化为某个变量的函数,再求解函数的最值,在寻底找高的过程中,优先选择长度为定值的线段参与运算。这样可以使函数解析式较为简单,便于分析.
方法:首选均值不等式或对勾函数,其实用二次函数配方法,最后选导数思想.
均值不等式 :变式:,
作用:当两个正数的积为定值时求出这两个正数的和的最小值;
当两个正数的和为定值时求出这两个正数的积的最大值!
注意:应用均值不等式求解最值时,应注意“一”正“二”定“三”相等
圆锥曲线经常用到的均值不等式形式:
1) (注意分 三种情况讨论)
2) ,当且仅当 时,等号成立
3) ,当且仅当 时等号成立.
4) ,当且仅当 时,等号成立.
5) 当且仅当 时等号成立.
6) 设,则由得t≥2,当且仅当k=1时取等号.因为在[2,+∞)单调递减,所以当t=2,即k=1时,S取得最大值.
【答案】
【解析】

【答案】B
【解析】

【答案】B
【解析】
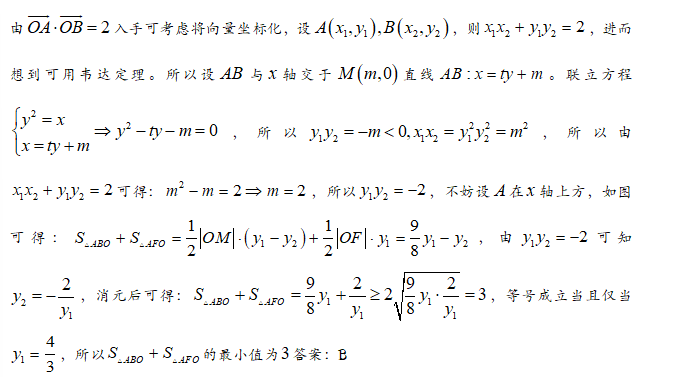

【答案】A
【解析】

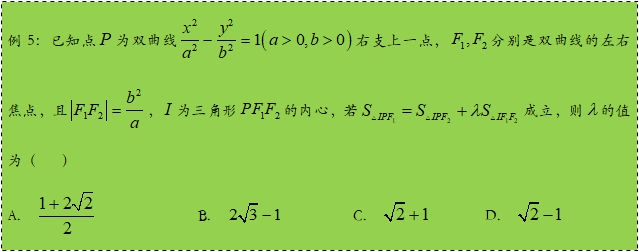
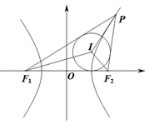
【答案】C
【解析】
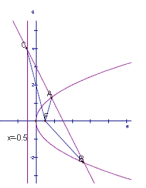
【答案】A
思路:

【解析】
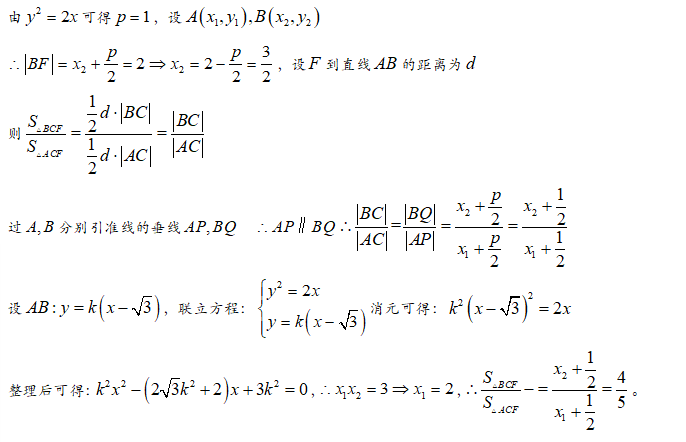
【证明】
一、单选题

【答案】C
【解析】
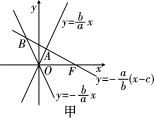
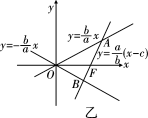
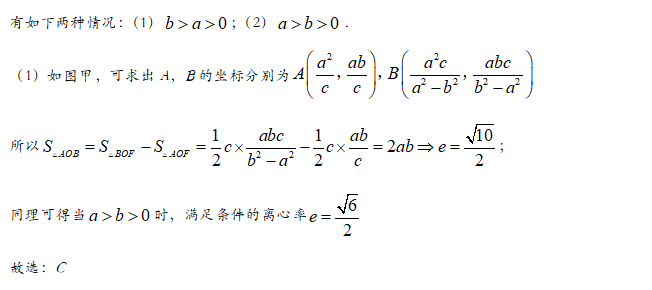

【答案】B
【解析】
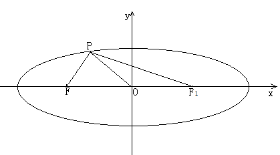


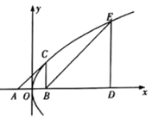
【答案】B
【解析】
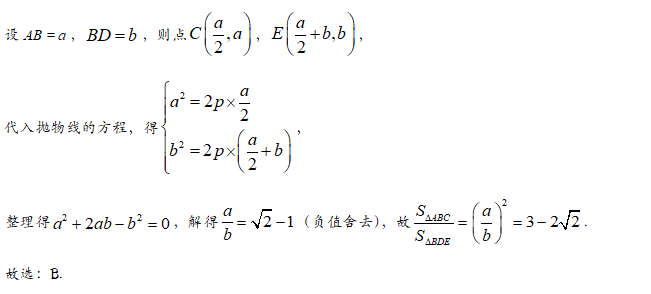

【答案】D
【解析】
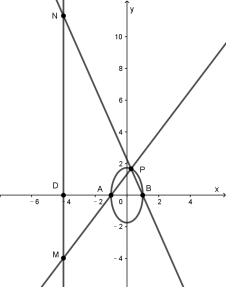
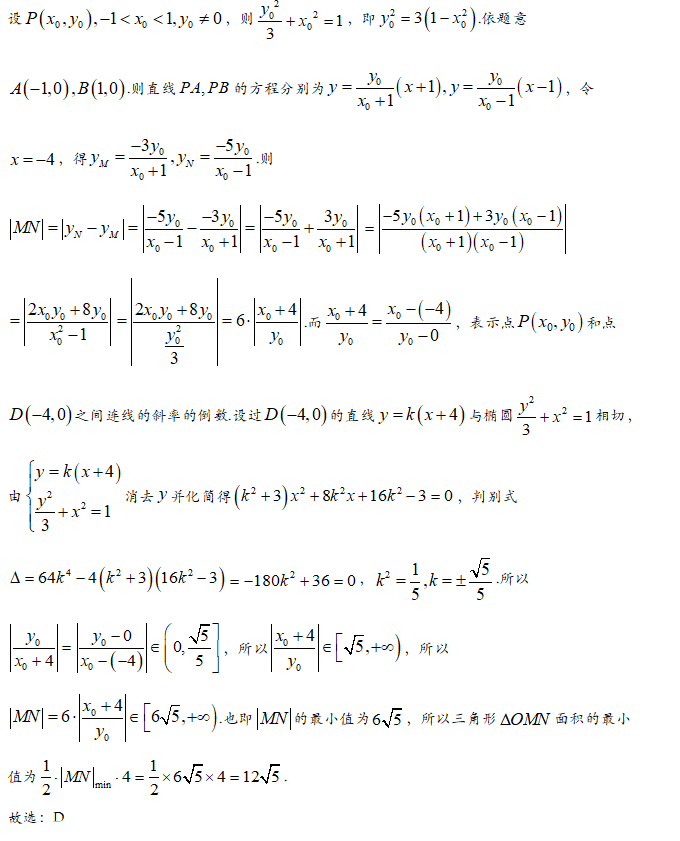
【答案】B
【解析】
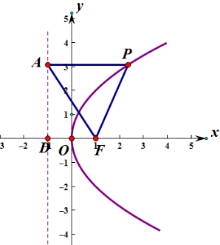


【答案】C

【答案】C

【答案】C

【答案】A

【答案】D
学科网][来源:学#科#网Z#X#X#K][来源:学科网]
【答案】C

【答案】C

【答案】D

【答案】A

【答案】C

【答案】A
【答案】B
【解析】
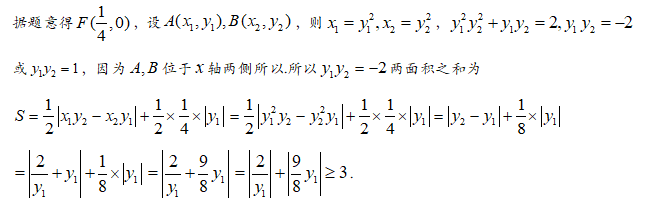

【答案】C
【解析】
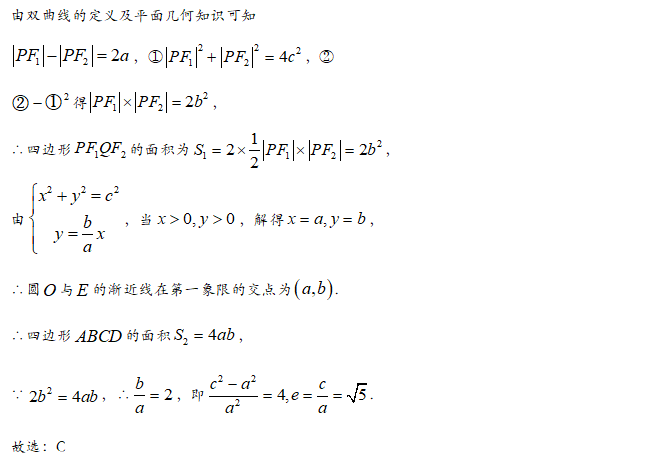

【答案】A
【解析】

一、填空题
【答案】3.
【解析】
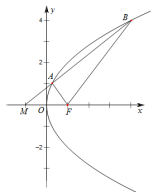
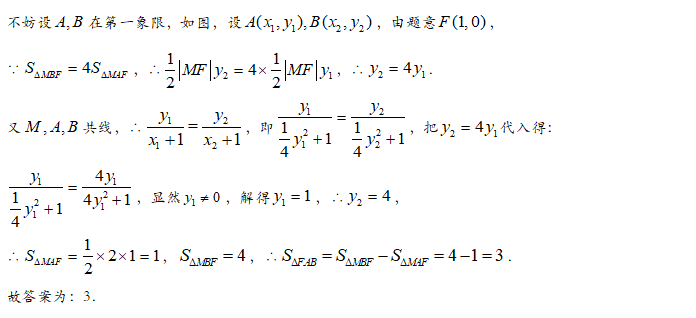
【答案】8
【解析】
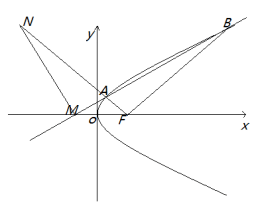
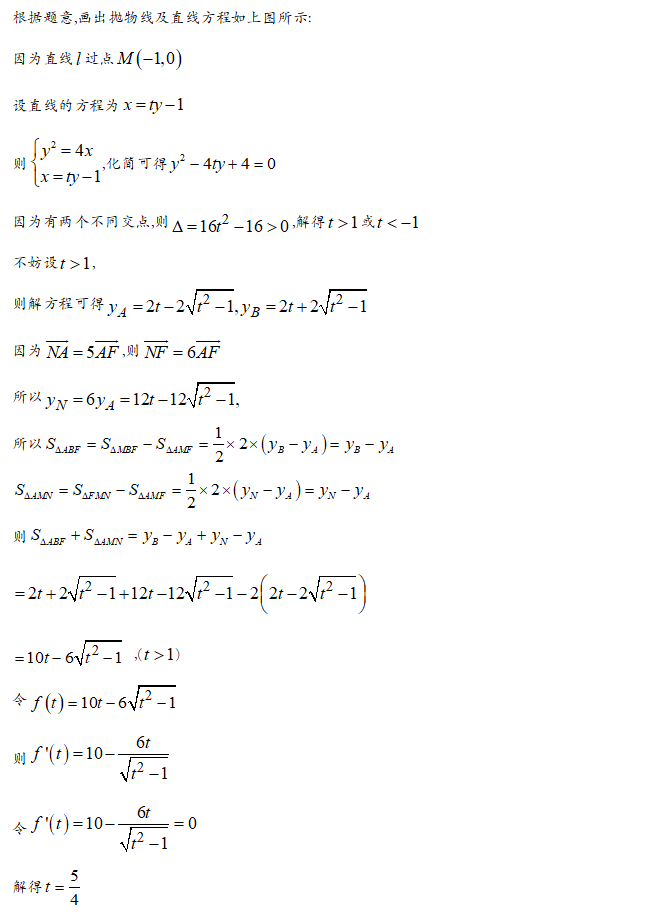
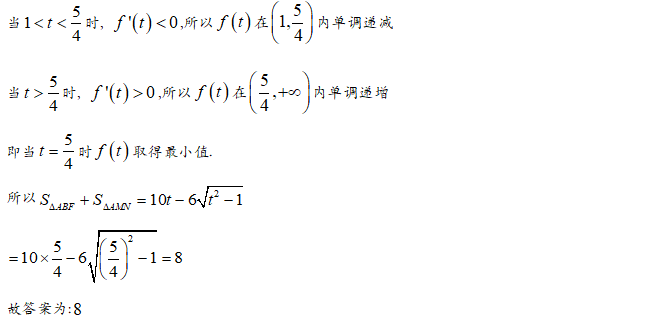
【答案】4
【解析】
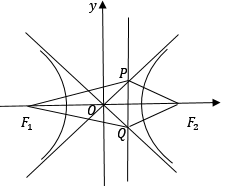
【答案】
【答案】3
【答案】
【答案】
【答案】
【解析】
圆锥曲线选填压轴小题之角度问题
必备基础
1.直线的倾斜角:在平面直角坐标系中,当直线l与x轴相交时,x轴正方向与直线l向上方向之间所成的角α叫做直线l的倾斜角.当直线l与x轴平行或重合时,规定它的倾斜角为0°,故直线的倾斜角α的取值范围为0°≤α