
NO.2
【初中数学常用模型最全汇总(精编)】
全等变换
平移:平行等线段(平行四边形)。
对称:角平分线或垂直或半角。
旋转:相邻等线段绕公共顶点旋转。
对称全等模型
说明:
以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。两边进行边或者角的等量代换,产生联系。垂直也可以做为轴进行对称全等。
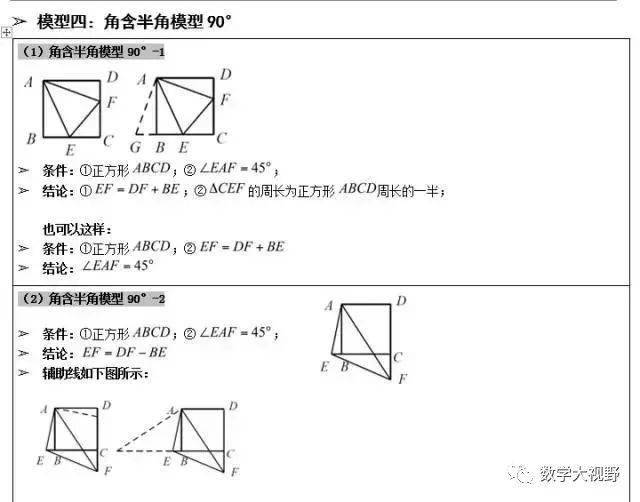
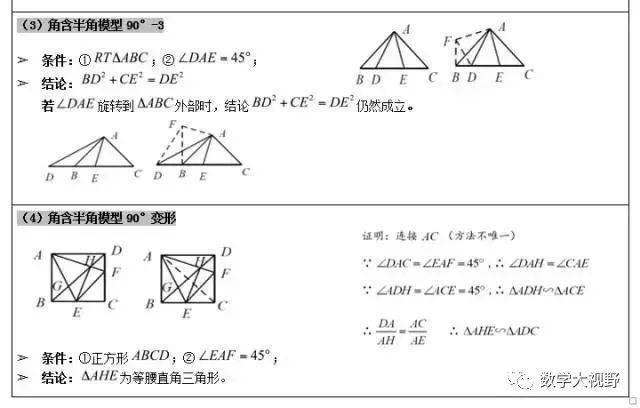
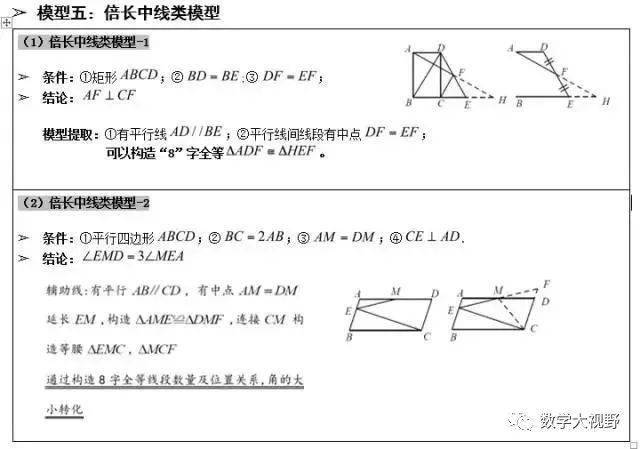
对称半角模型
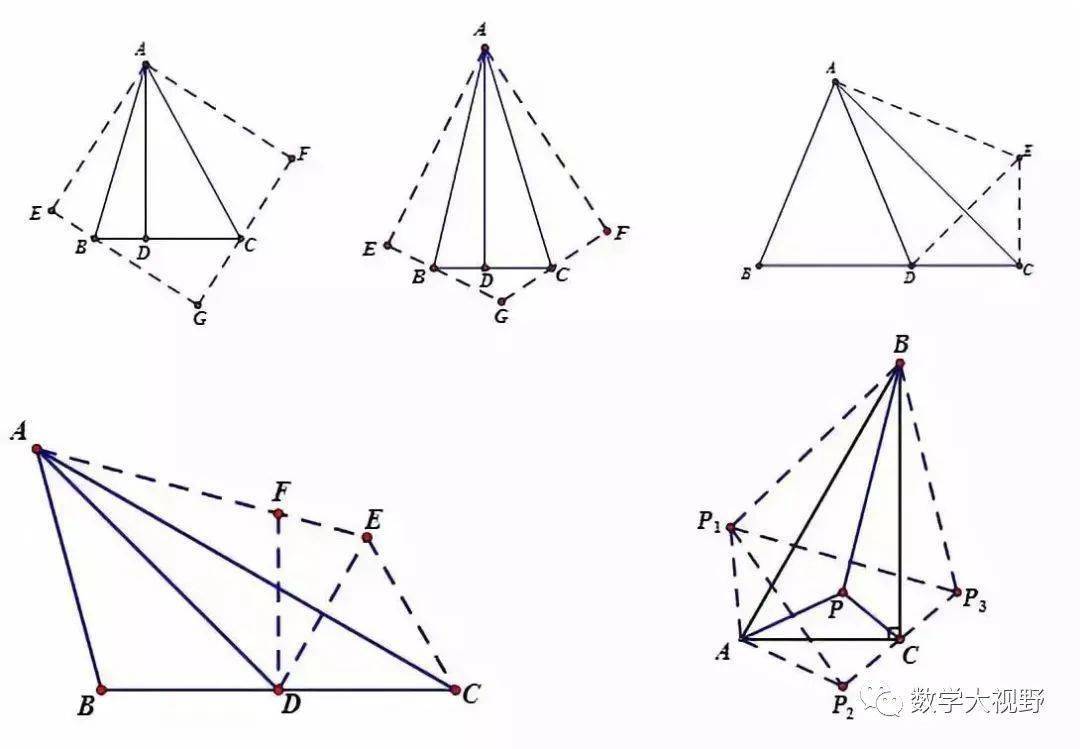
说明:
上图依次是45°、30°、22.5°、15°及有一个角是30°直角三角形的对称(翻折),翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
旋转全等模型
半角:有一个角含1/2角及相邻线段。
自旋转:有一对相邻等线段,需要构造旋转全等。
共旋转:有两对相邻等线段,直接寻找旋转全等。
中点旋转:倍长中点相关线段转换成旋转全等问题。
旋转半角模型
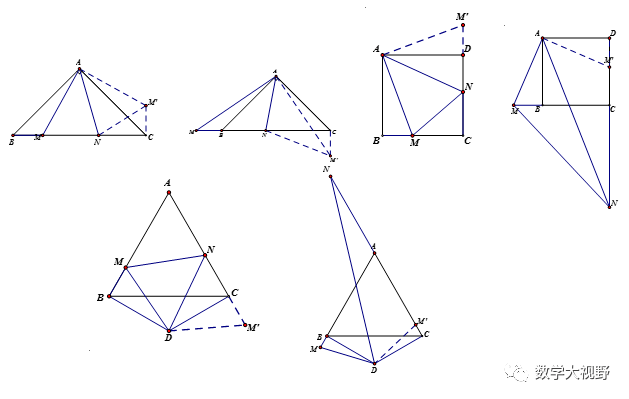
说明:
旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
自旋转变换
构造方法:
遇60度旋60度,造等边三角形;
遇90度旋90度,造等腰直角;
遇等腰旋顶点,造旋转全等;
遇中点旋180度,造中心对称。
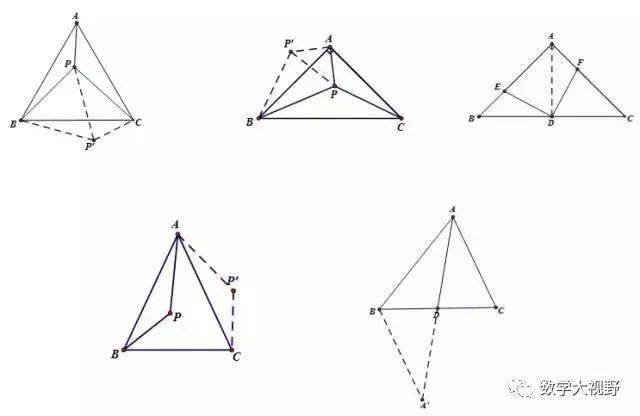
共旋转模型
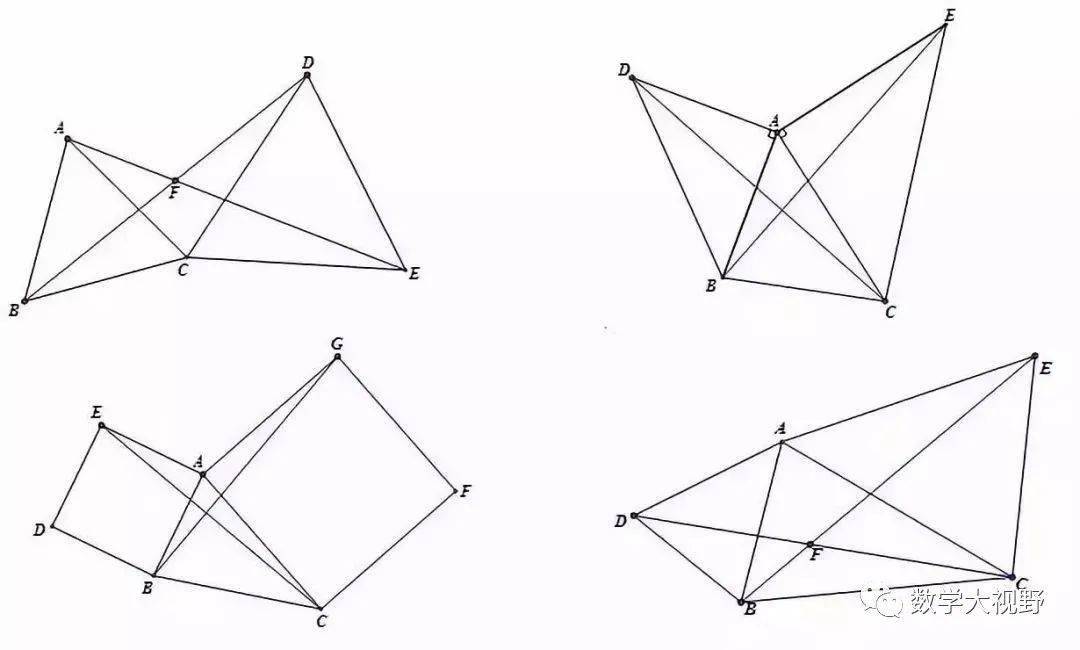
说明:
旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。通过“8”字模型可以证明。
模型变形
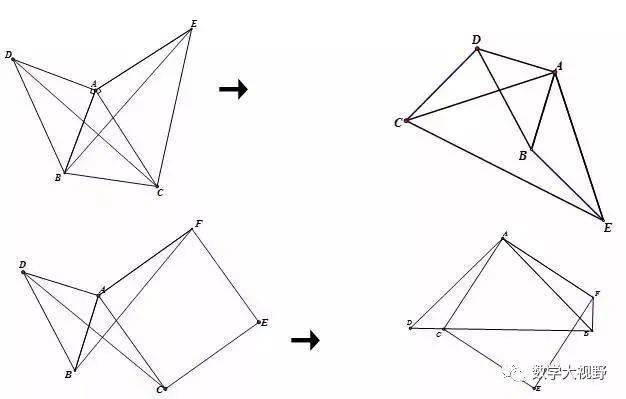
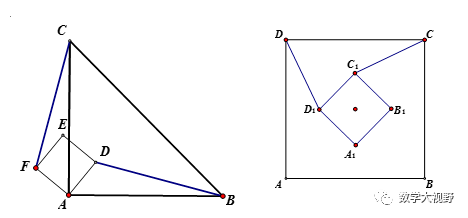
说明:
模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形的混用。
当遇到复杂图形找不到旋转全等时,先找两个正多边形或者等腰三角形的公共顶点,围绕公共顶点找到两组相邻等线段,分组组成三角形证全等。
中点旋转模型
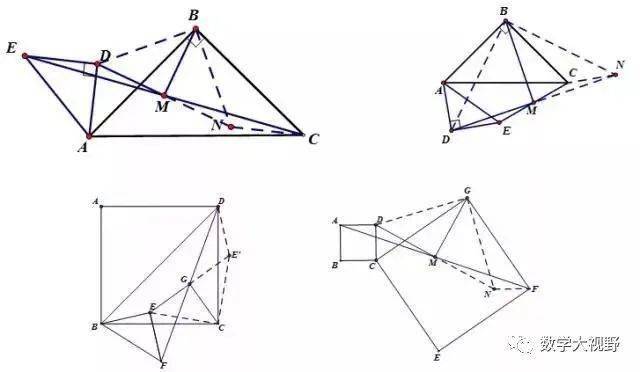
说明:
两个正方形、两个等腰直角三角形或者一个正方形一个等腰直角三角形及两个图形顶点连线的中点,证明另外两个顶点与中点所成图形为等腰直角三角形。证明方法是倍长所要证等腰直角三角形的一直角边,转化成要证明的等腰直角三角形和已知的等腰直角三角形(或者正方形)公旋转顶点,通过证明旋转全等三角形证明倍长后的大三角形为等腰直角三角形从而得证。
几何最值模型
对称最值(两点间线段最短)
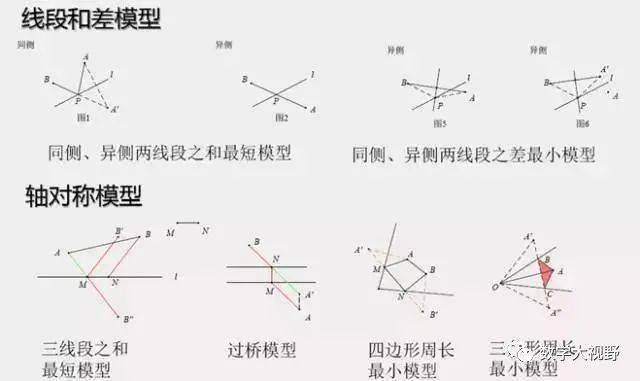
对称最值(点到直线垂线段最短)
说明:
通过对称进行等量代换,转换成两点间距离及点到直线距离。
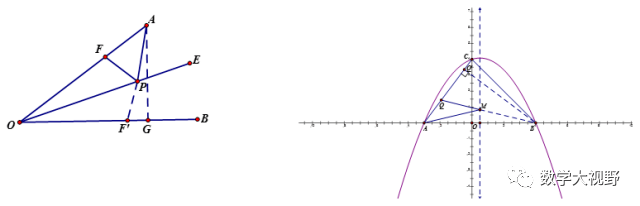
旋转最值(共线有最值)
说明:
找到与所要求最值相关成三角形的两个定长线段,定长线段的和为最大值,定长线段的差为最小值。
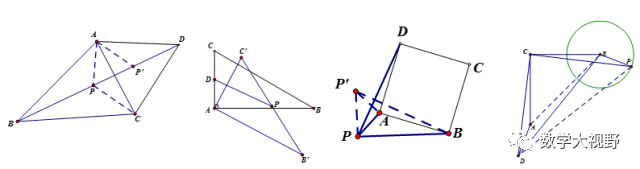
简拼模型
三角形→四边形
四边形→四边形
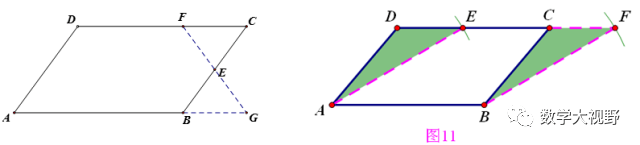
说明:
剪拼主要是通过中点的180度旋转及平移改变图形的形状。
矩形→正方形
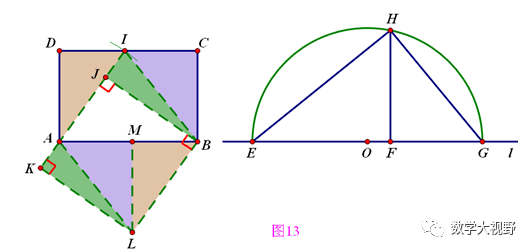
说明:
通过射影定理找到正方形的边长,通过平移与旋转完成形状改变
正方形+等腰直角三角形→正方形
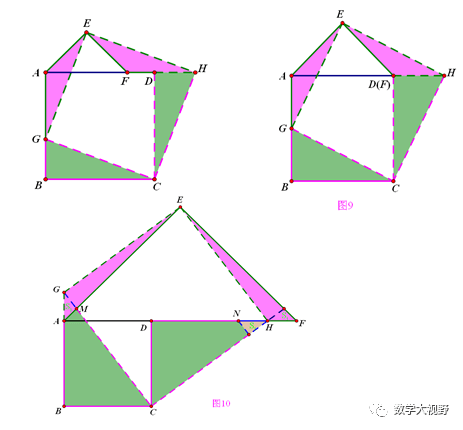
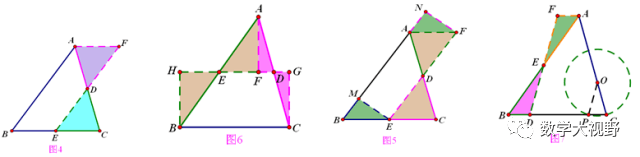
面积等分
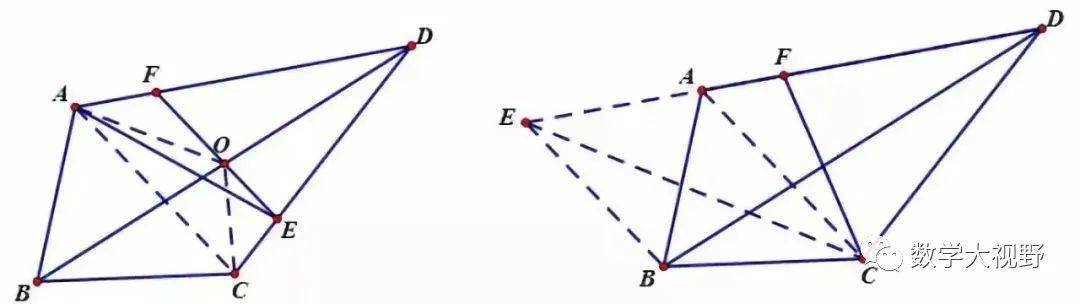
旋转相似模型
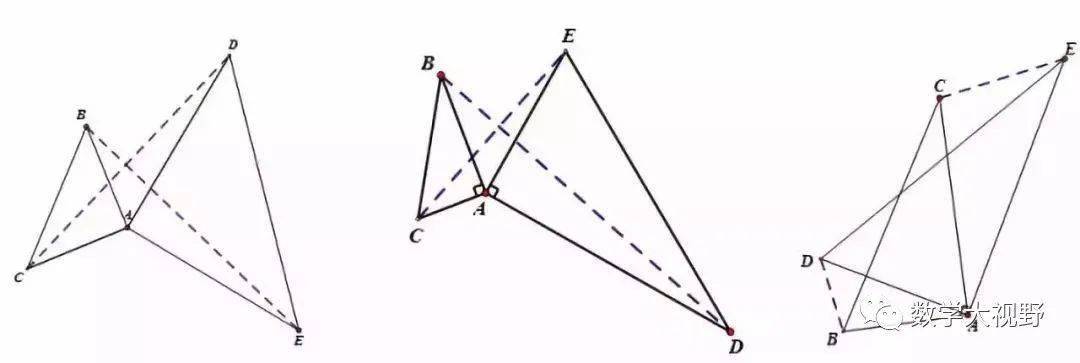
说明:
两个等腰直角三角形成旋转全等,两个有一个角是300角的直角三角形成旋转相似。
推广:两个任意相似三角形旋转成一定角度,成旋转相似。第三边所成夹角符合旋转“8”字的规律。
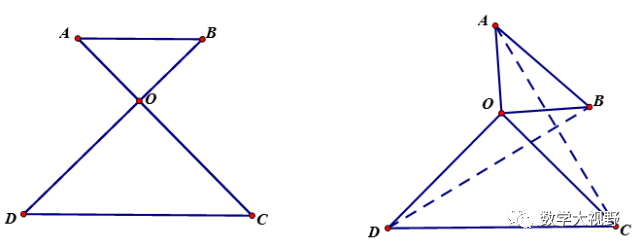
相似模型
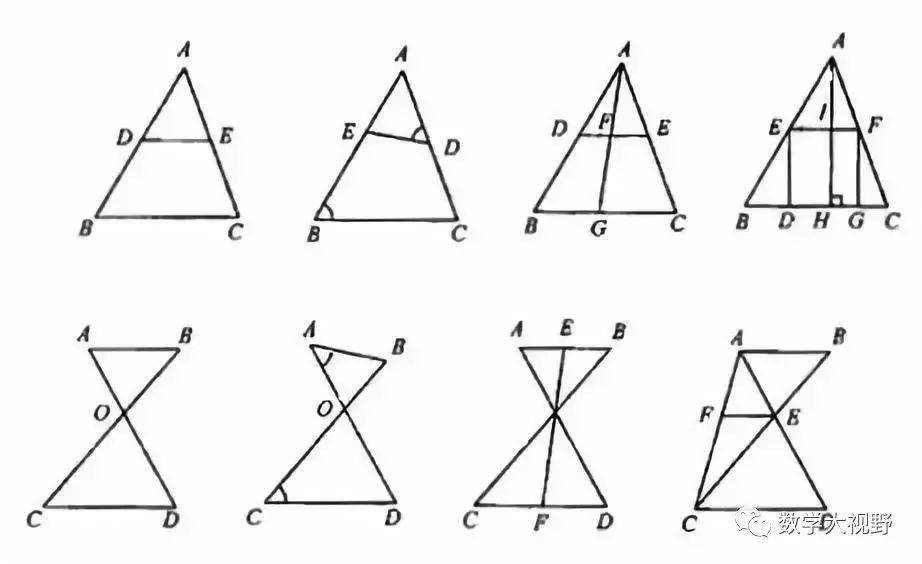
说明:
注意边和角的对应,相等线段或者相等比值在证明相似中起到通过等量代换来构造相似三角形的作用。
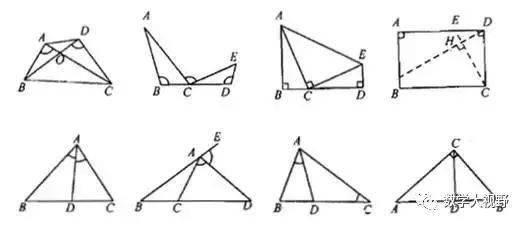
说明:
(1)三垂直到一线三等角的演变,三等角以30度、45度、60度形式出现的居多。
(2)内外角平分线定理到射影定理的演变,注意之间的相同与不同之处。另外,相似、射影定理、相交弦定理(可以推广到圆幂定理)之间的比值可以转换成乘积,通过等线段、等比值、等乘积进行代换,进行证明得到需要的结论。
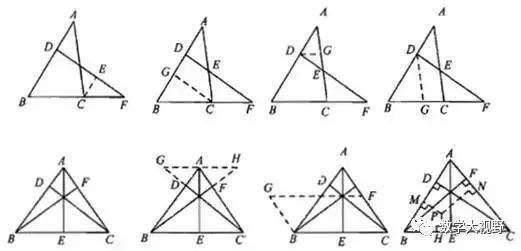
说明:
相似证明中最常用的辅助线是作平行,根据题目的条件或者结论的比值来作相应的平行线。


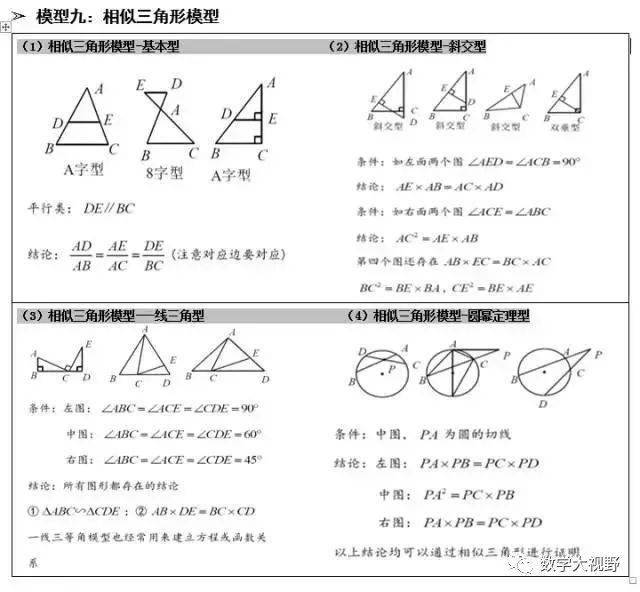
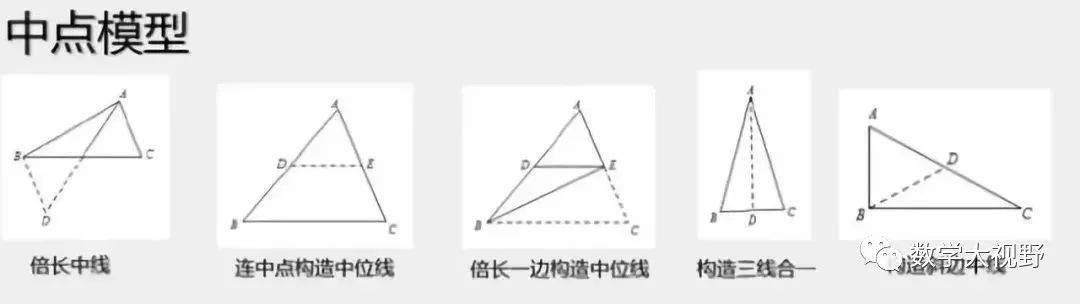
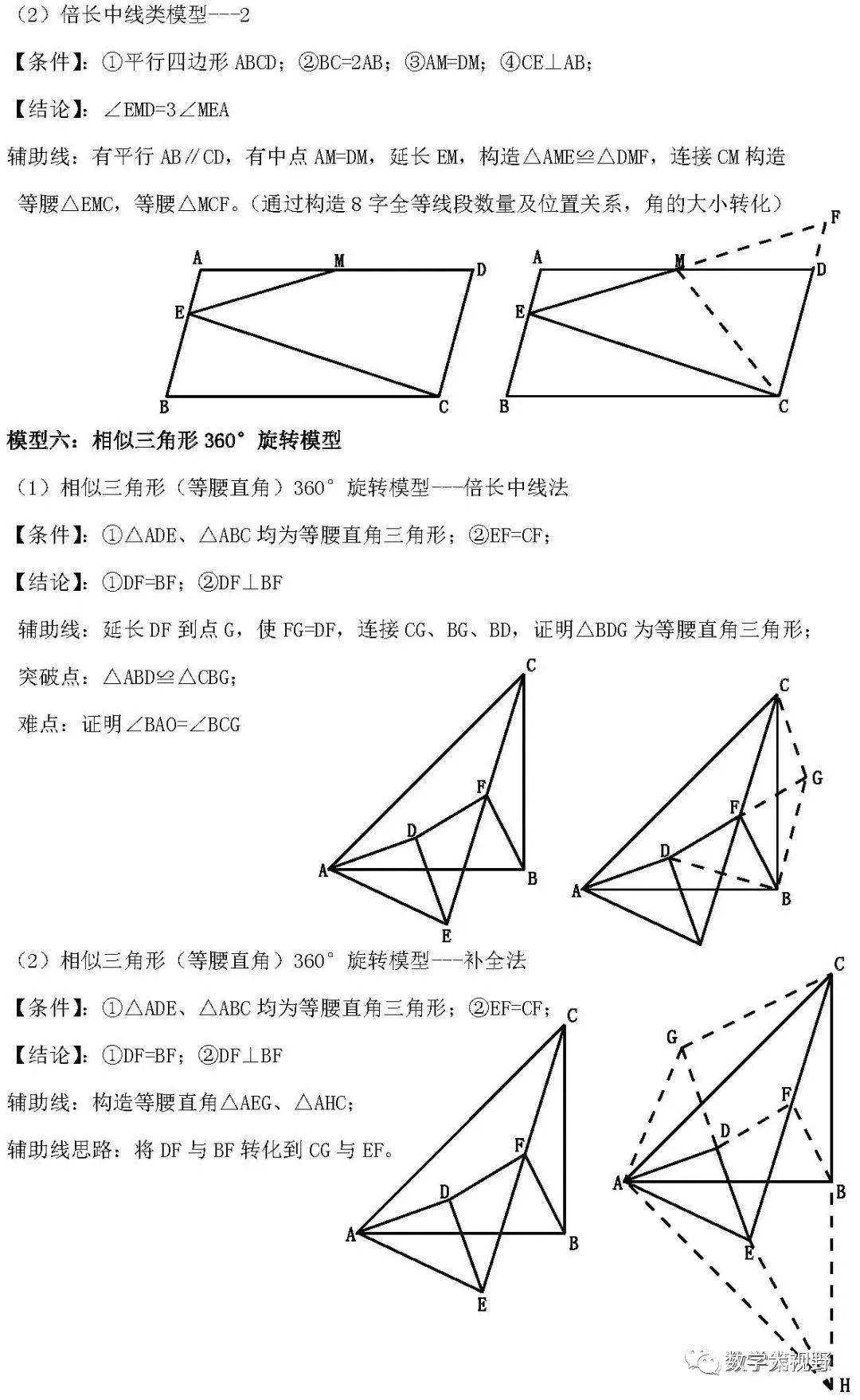
中点模型
【模型1】倍长
1、 倍长中线;2、倍长类中线;3、中点遇平行延长相交
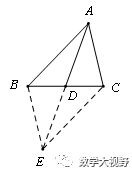
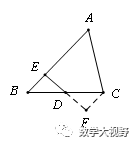
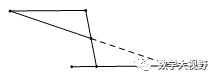
【模型2】遇多个中点,构造中位线
1、 直接连接中点;2、连对角线取中点再相连
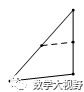
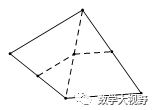
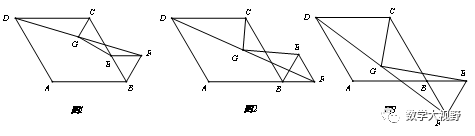
【例】在菱形ABCD和正三角形BEF中,∠ABC=60°,G是DF的中点,连接GC、GE.
(1)如图1,当点E在BC边上时,若AB=10,BF=4,求GE的长;
(2)如图2,当点F在AB的延长线上时,线段GC、GE有怎样的数量和位置关系,写出你的猜想;并给予证明;
(3)如图3,当点F在CB的延长线上时,(2)问中关系还成立吗?写出你的猜想,并给予证明.
角平分线模型
【模型1】构造轴对称
【模型2】角平分线遇平行构造等腰三角形
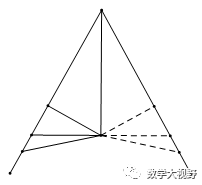
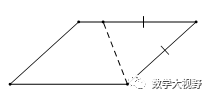
【例】如图,平行四边形ABCD中,AE平分∠BAD交BC边于E,EF⊥AE交CD边于F,交AD边于H,延长BA到点G,使AG=CF,连接GF.若BC=7,DF=3,EH=3AE,则GF的长为
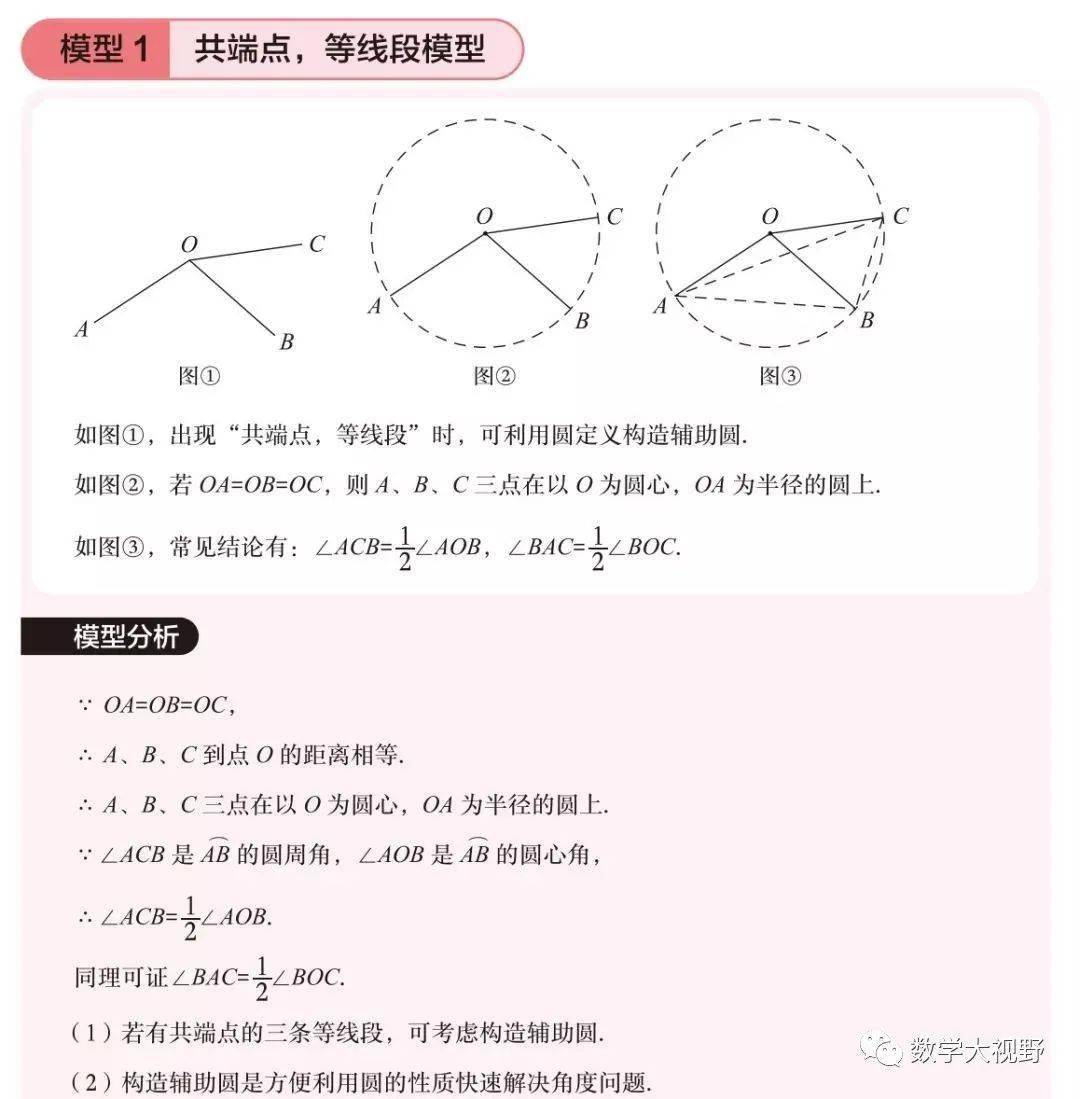
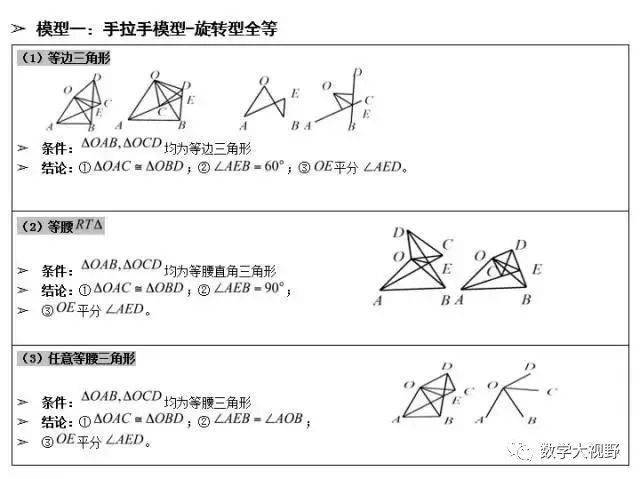
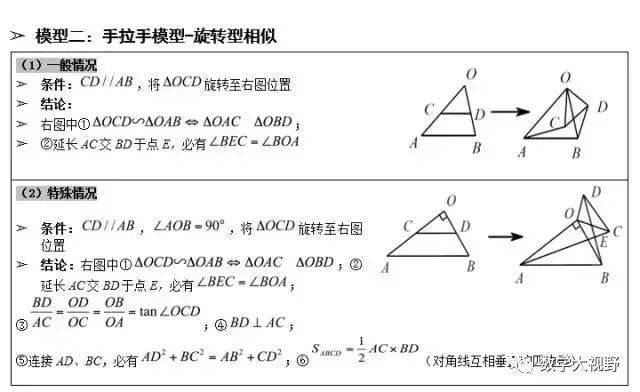
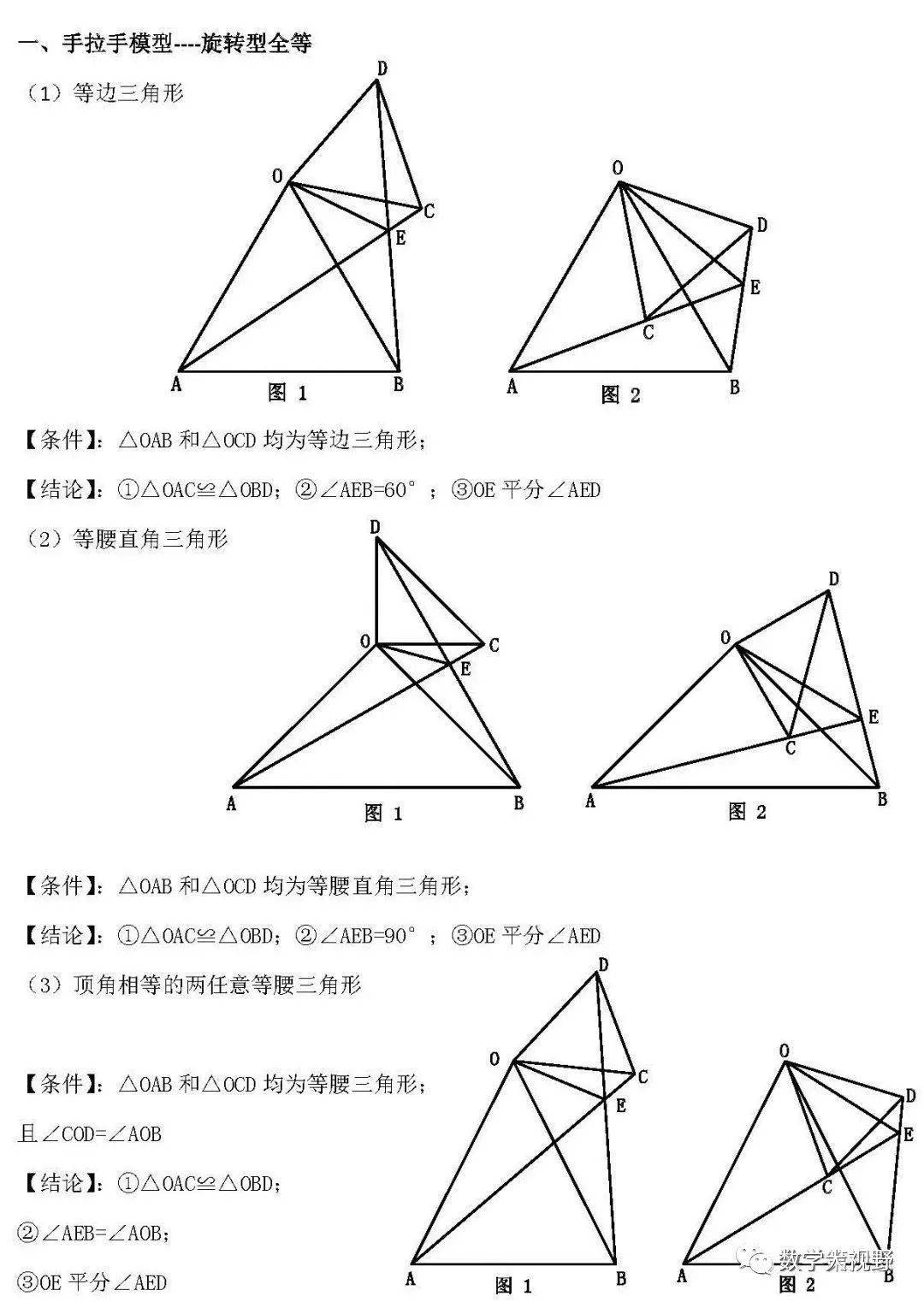
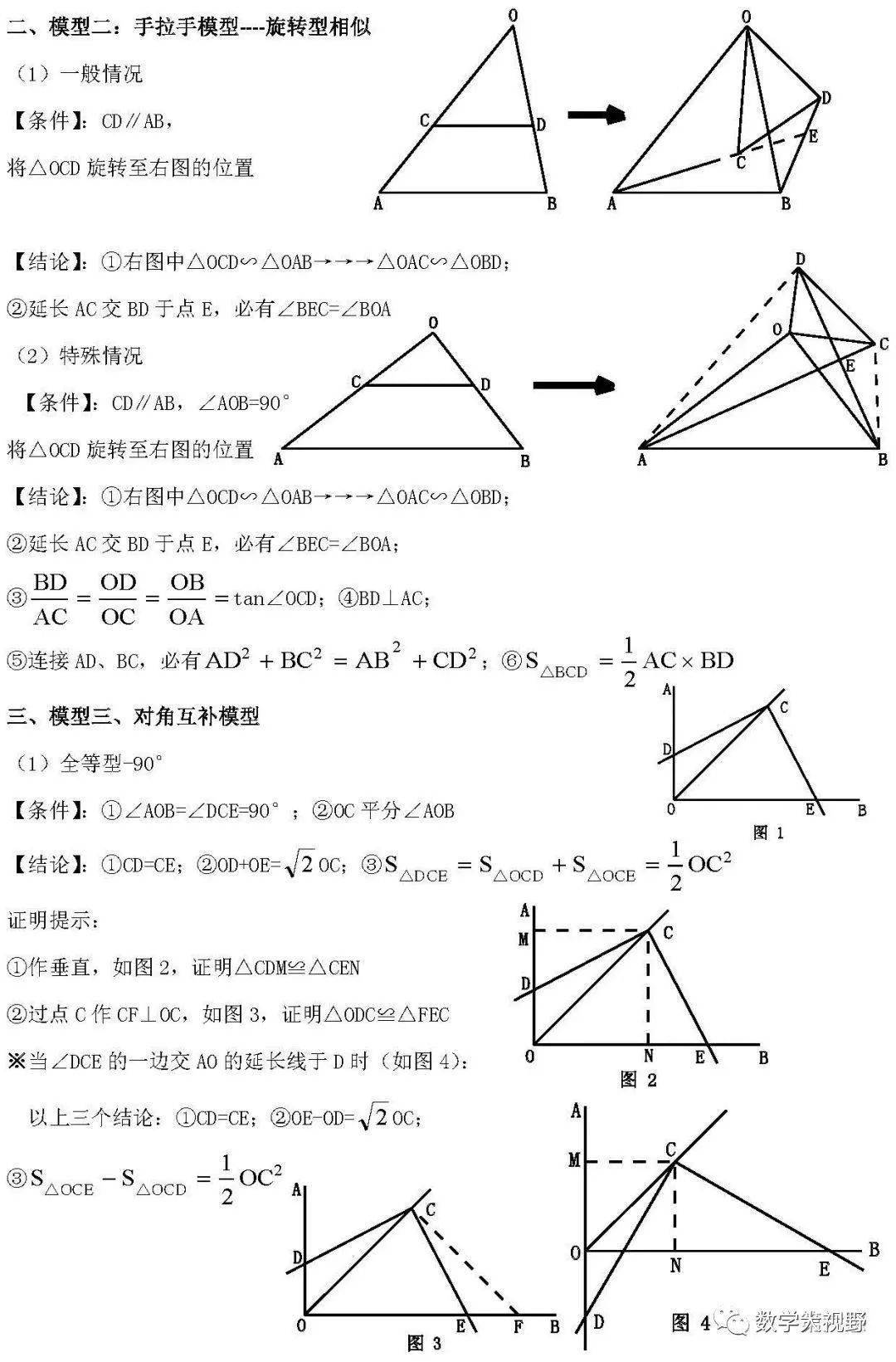
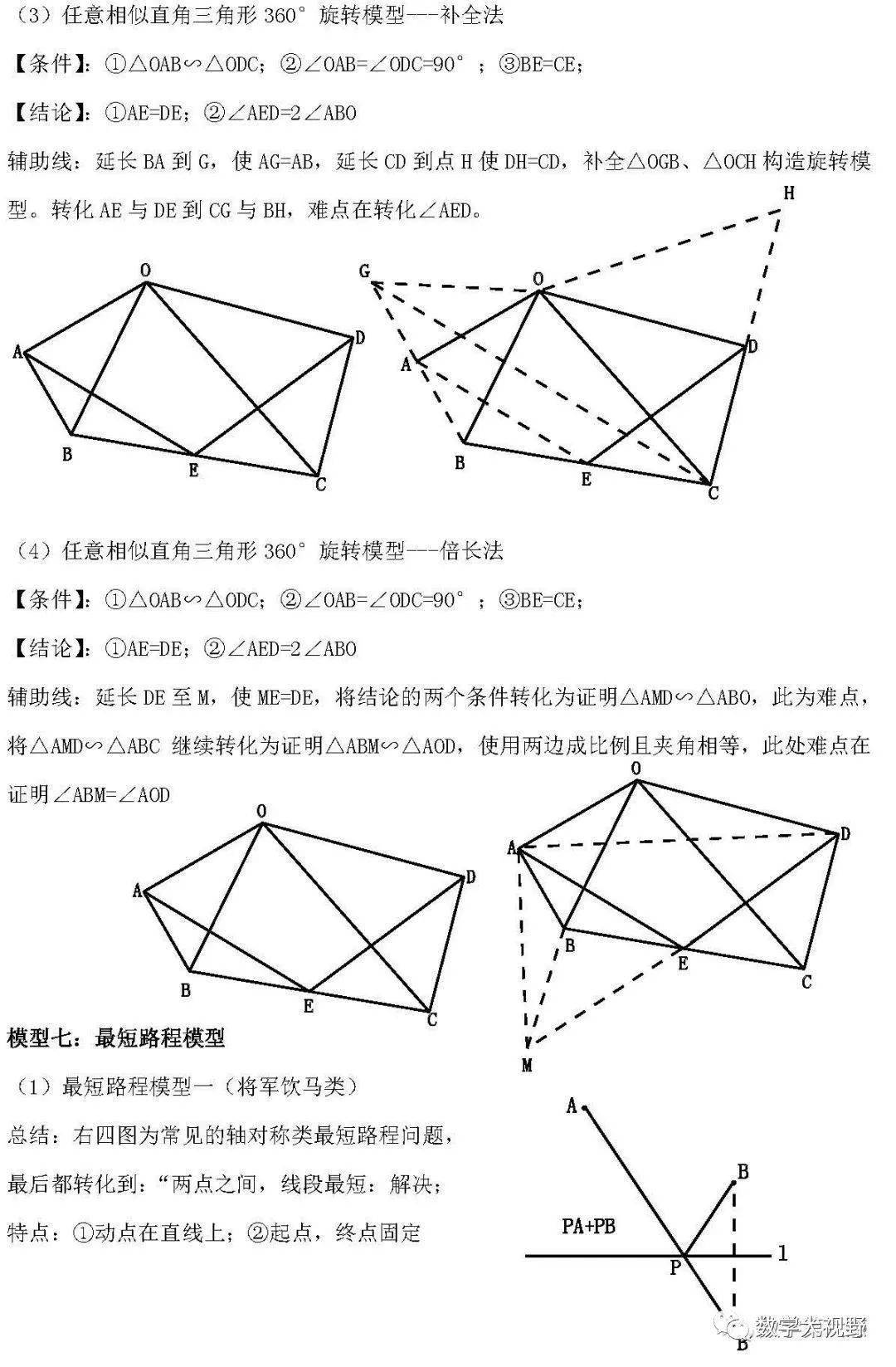
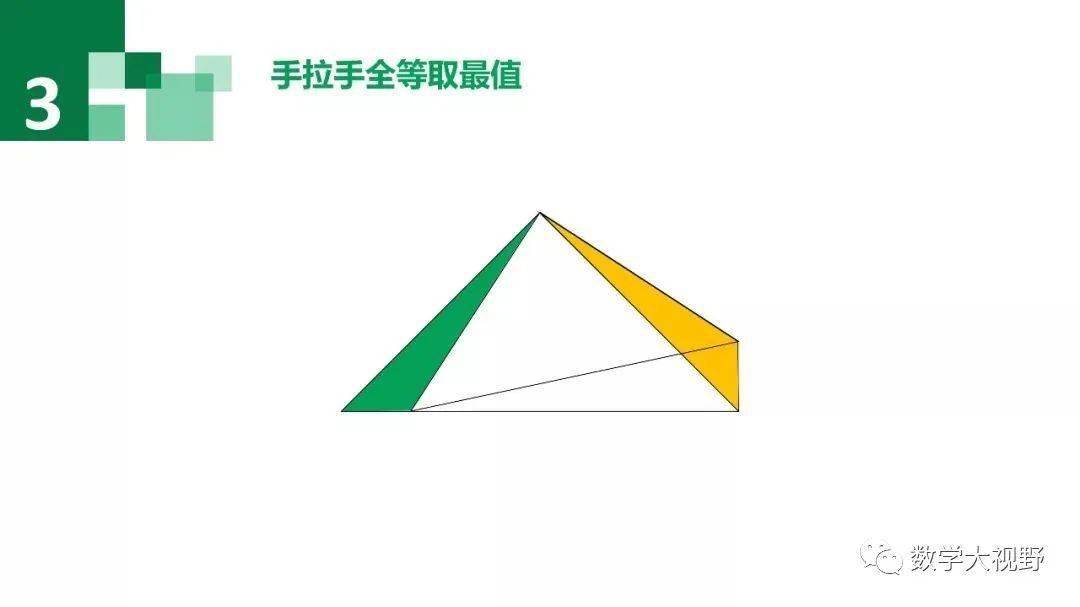
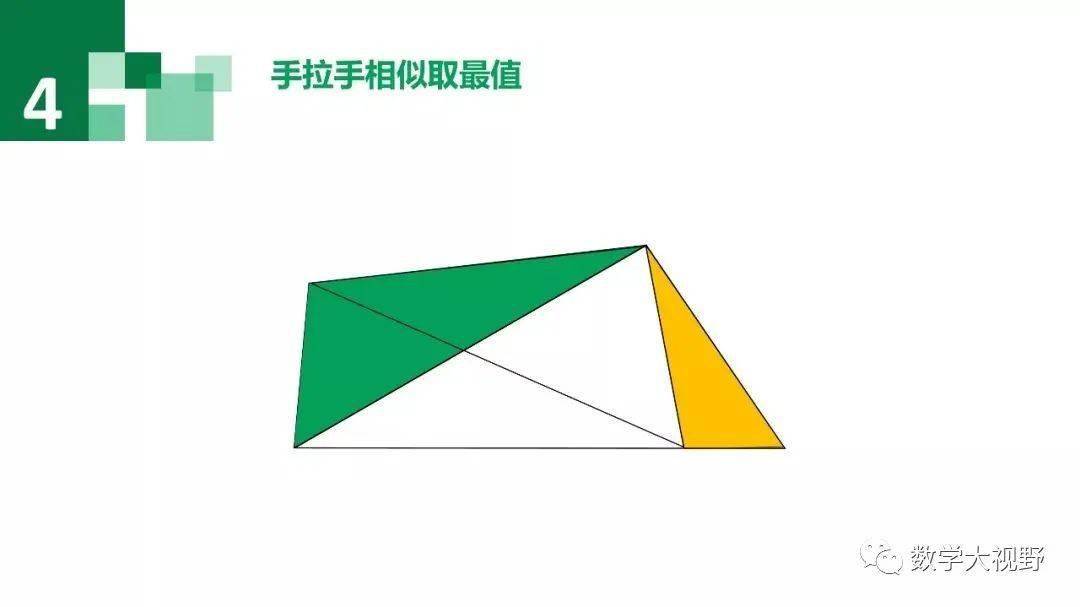
手拉手模型
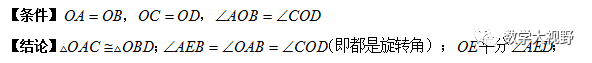
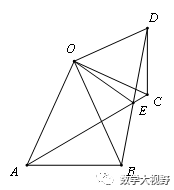
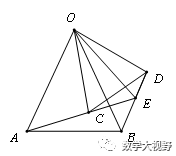
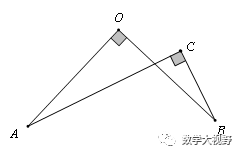
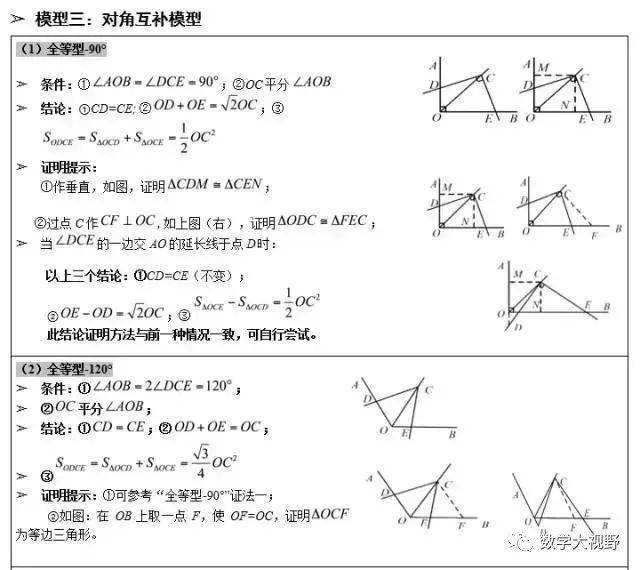
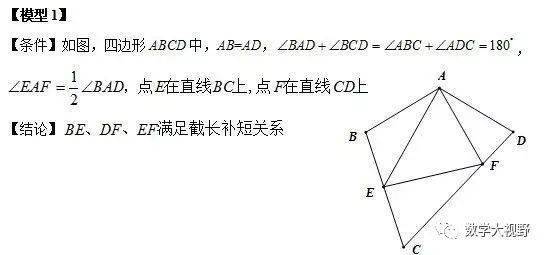
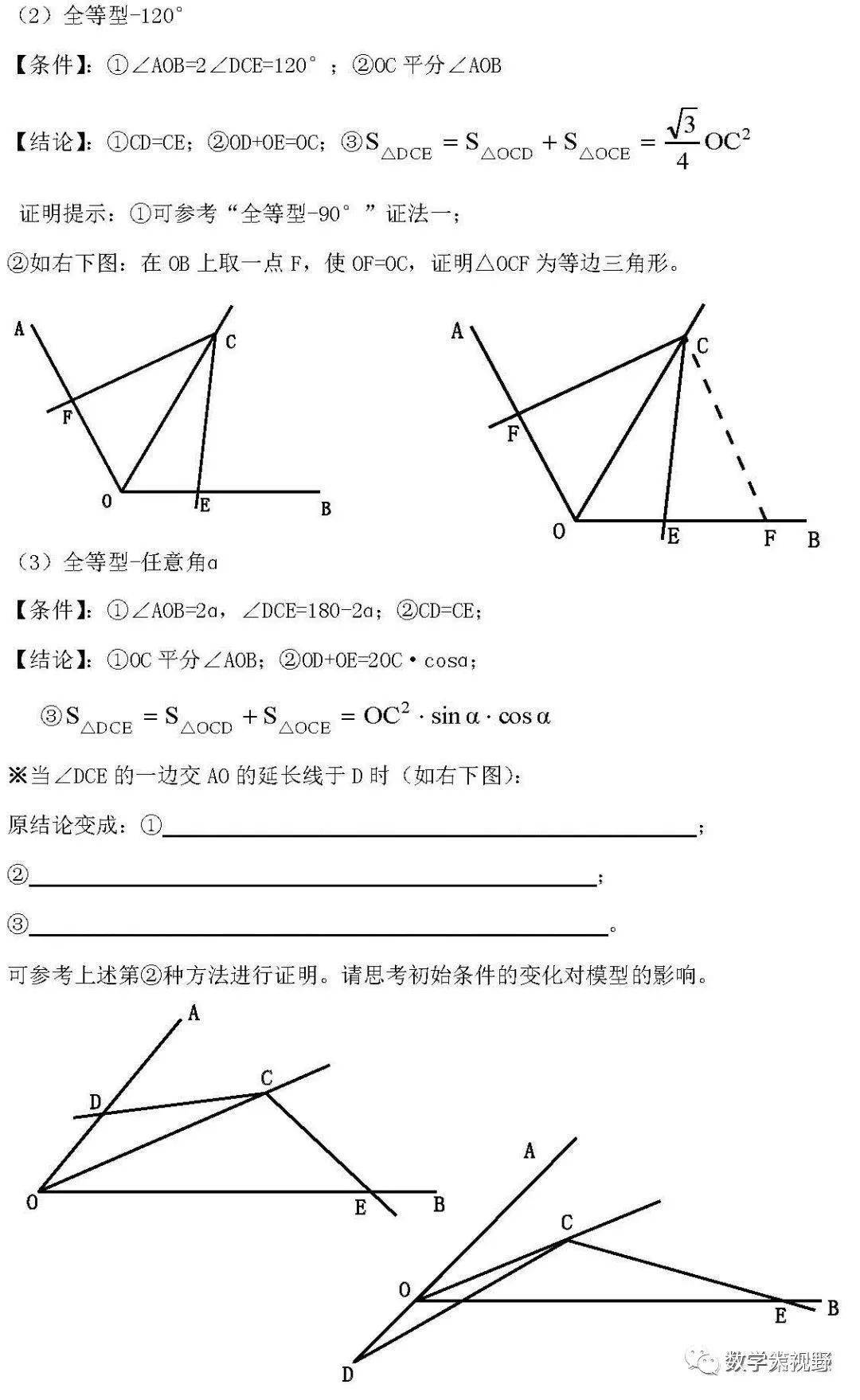
邻边相等的对角互补模型
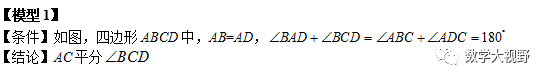
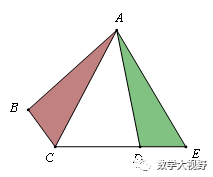
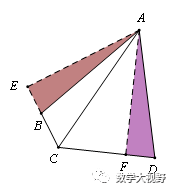
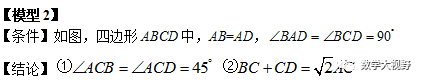
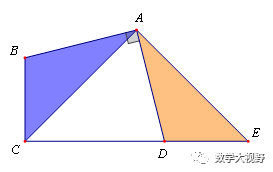
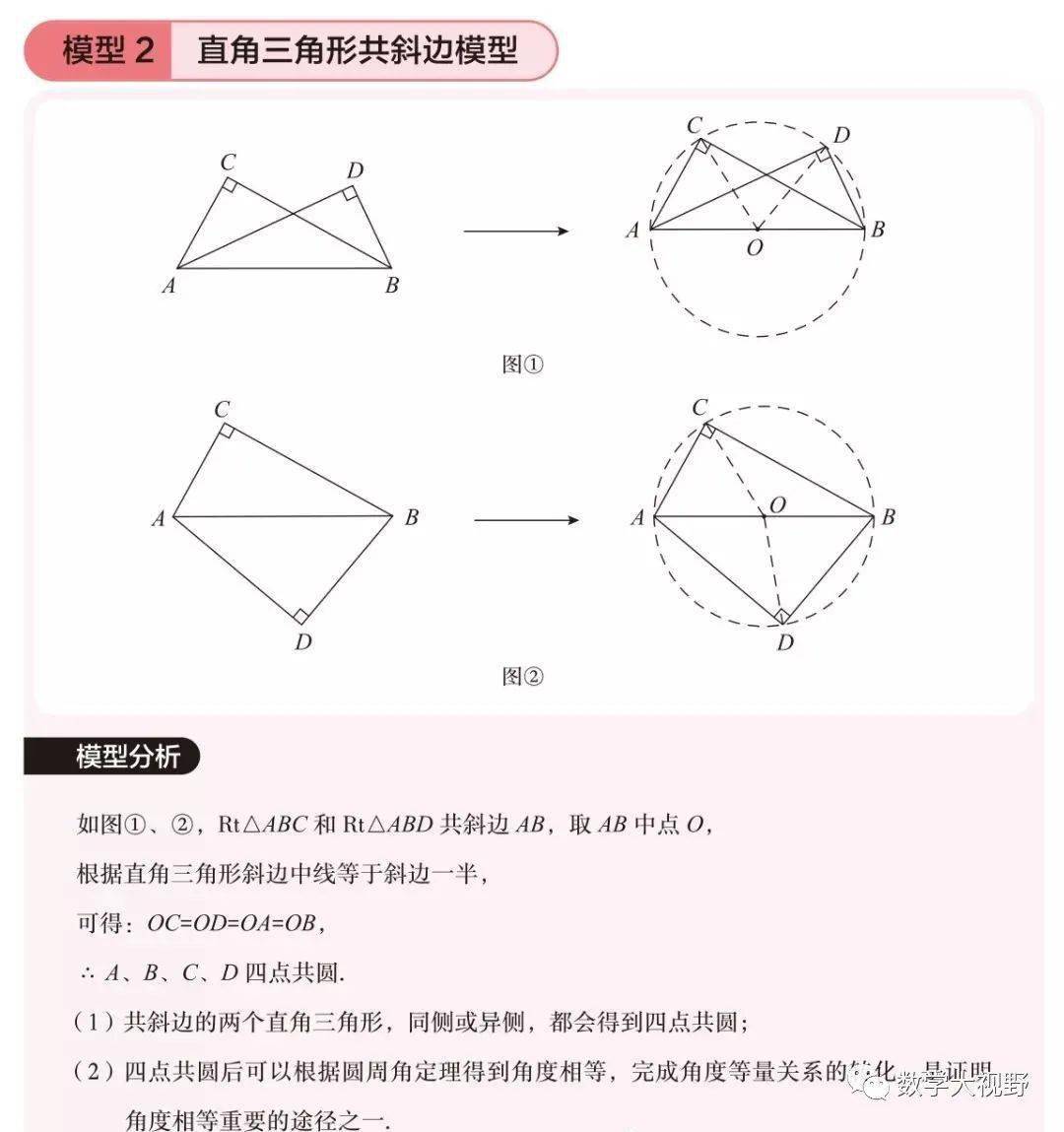
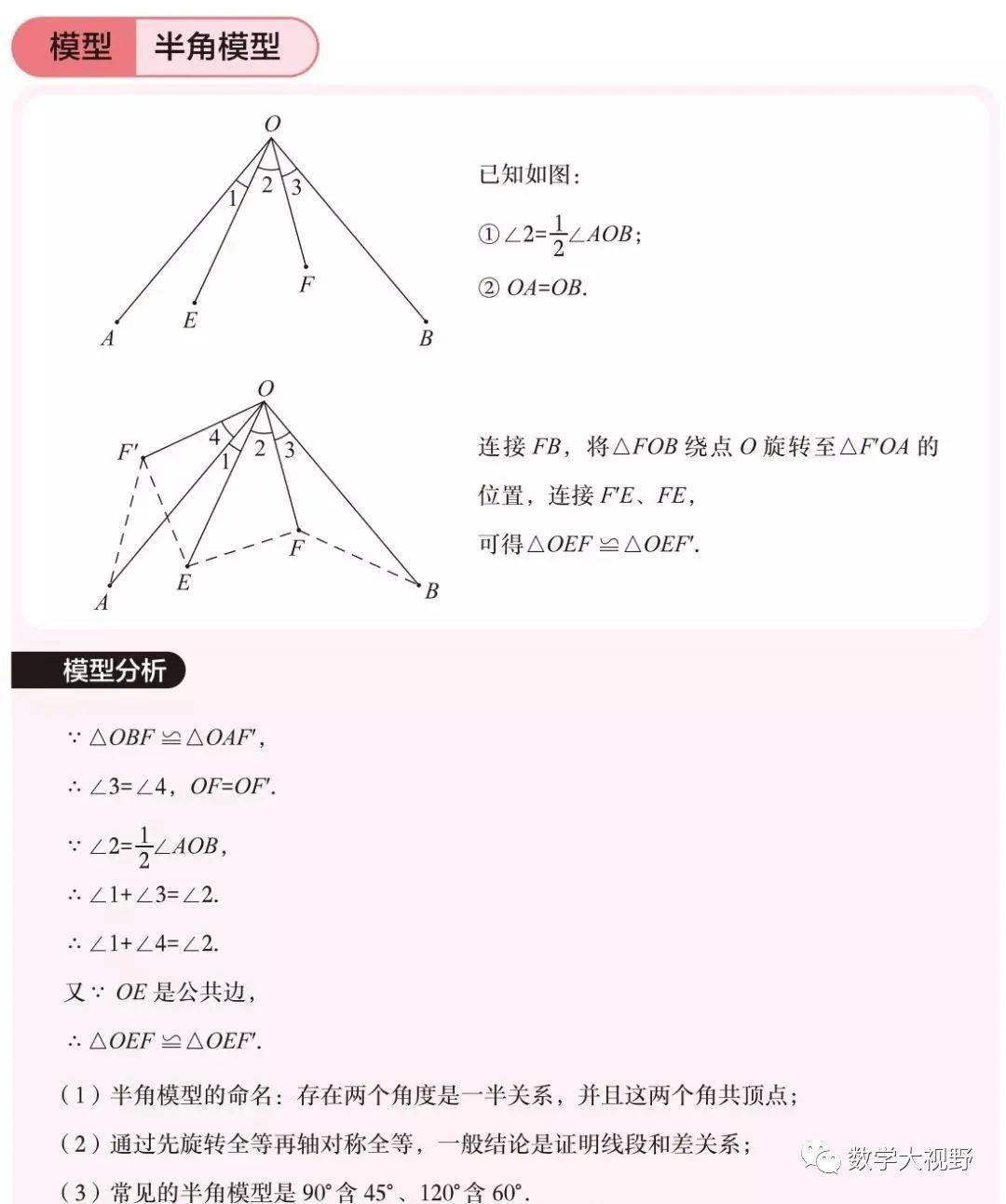
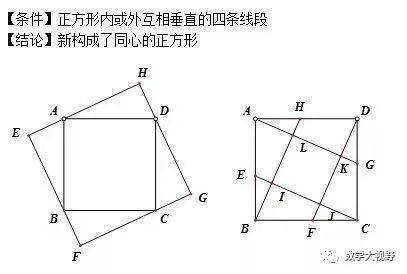
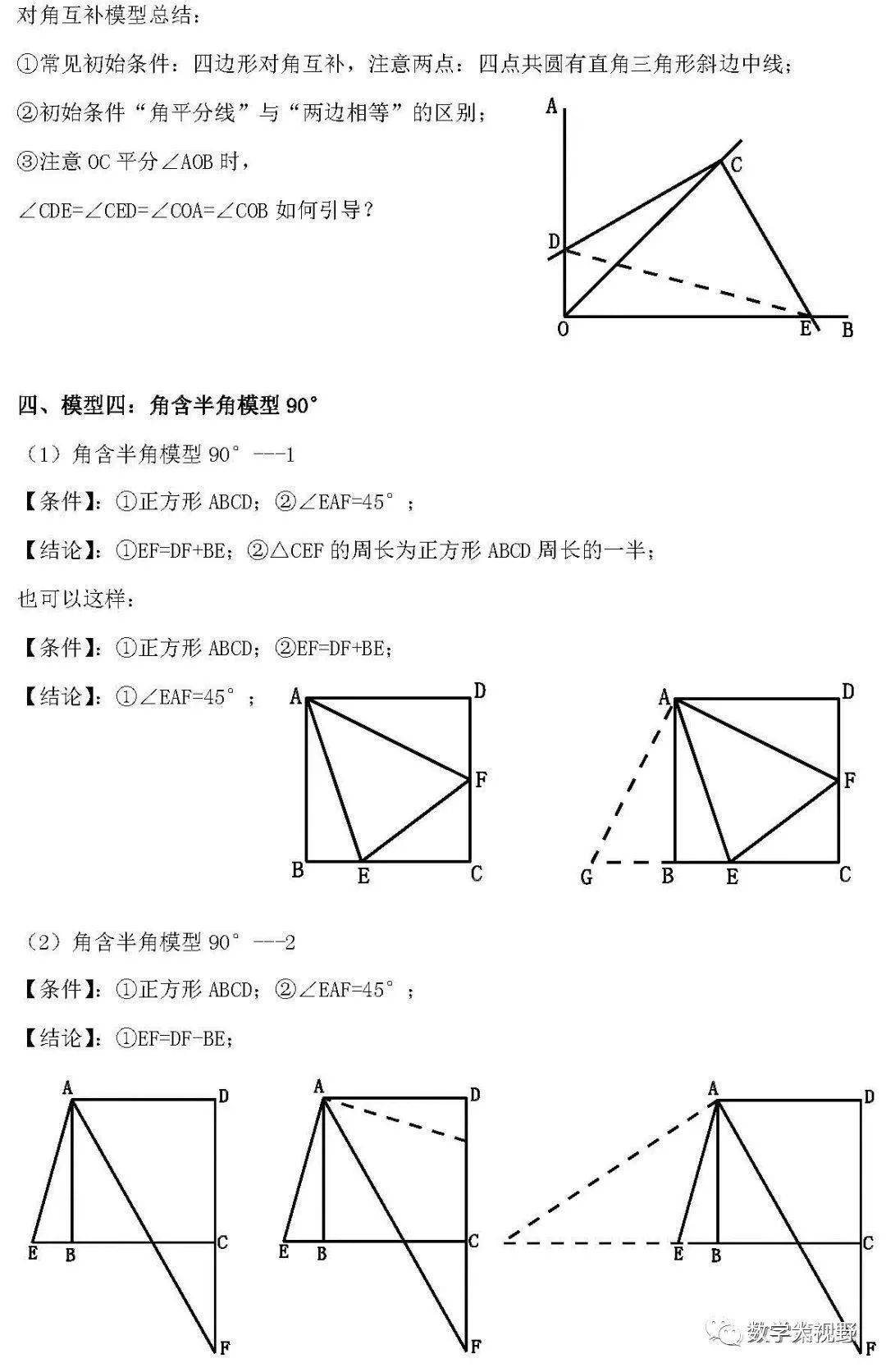
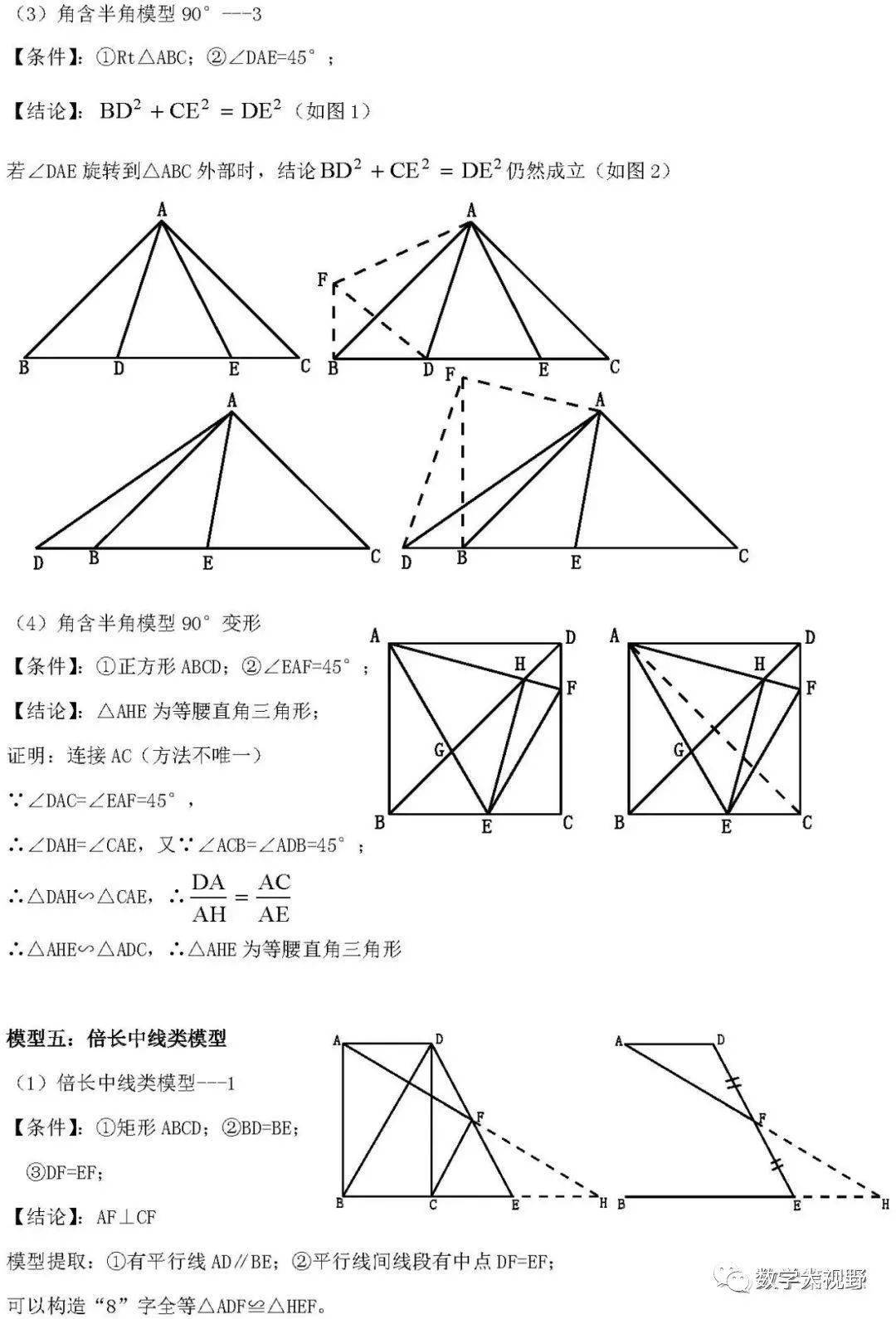
半角模型
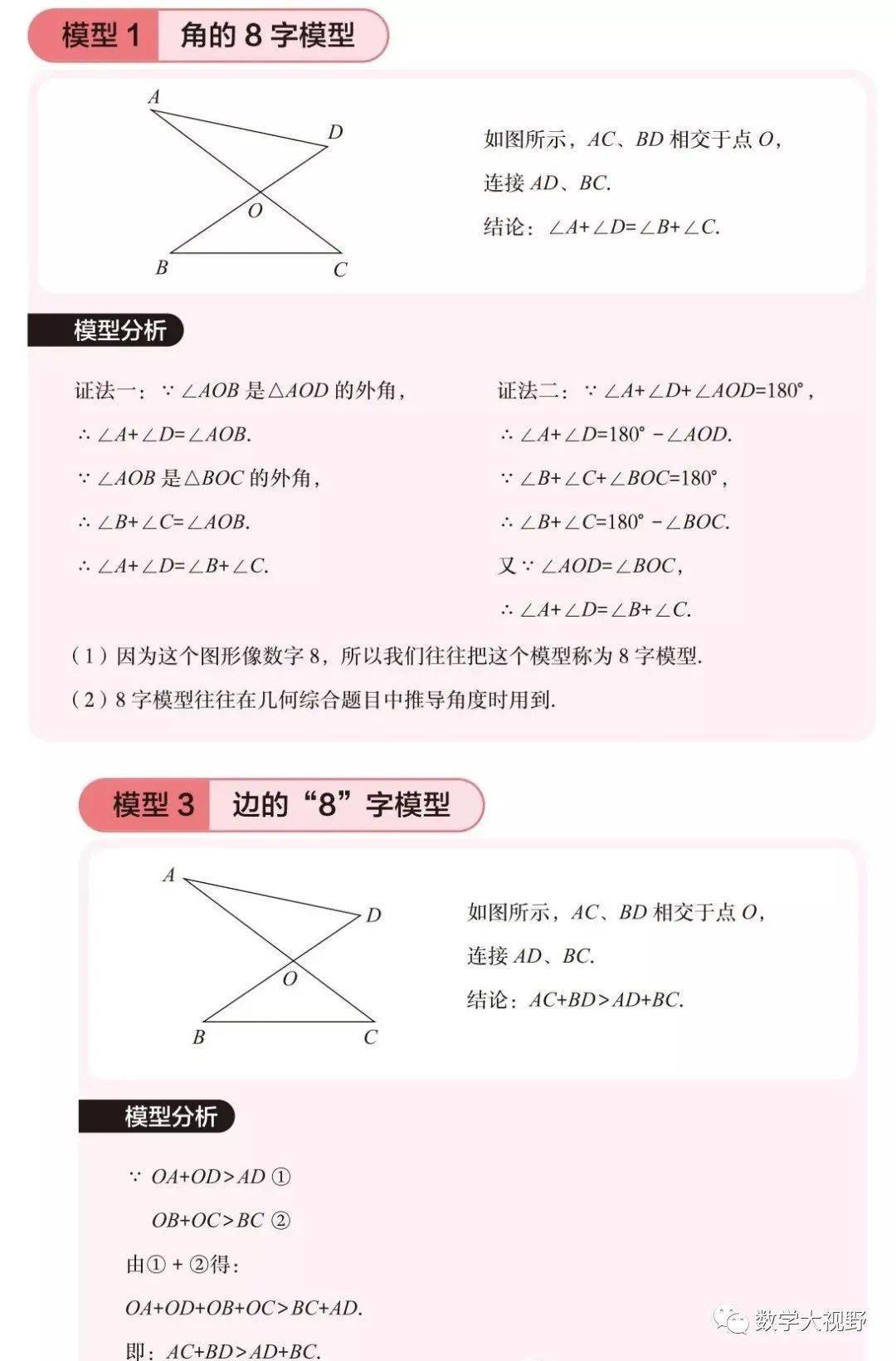
弦图模型
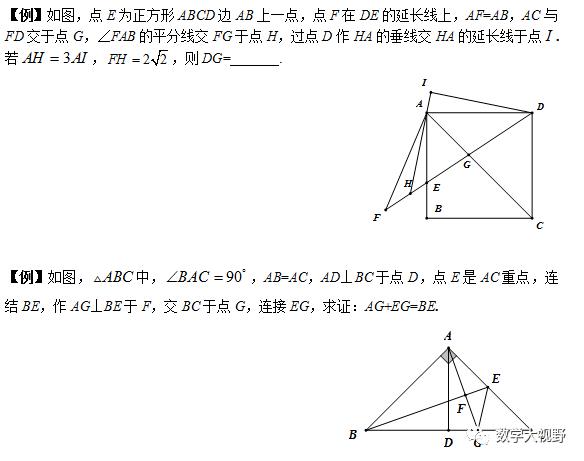
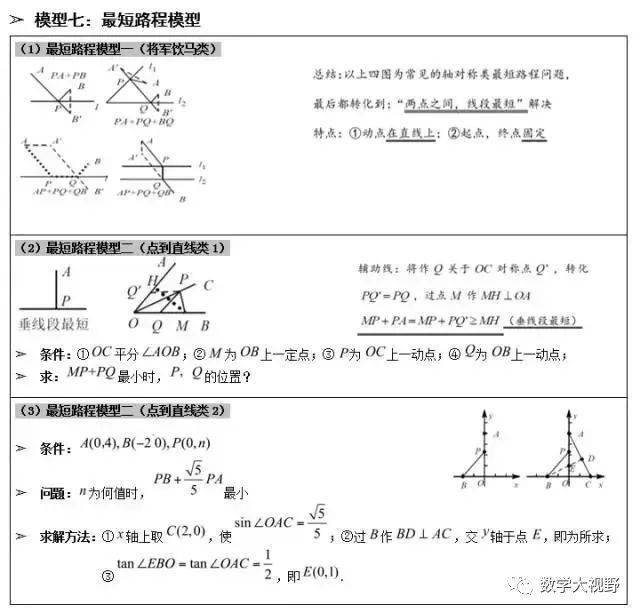
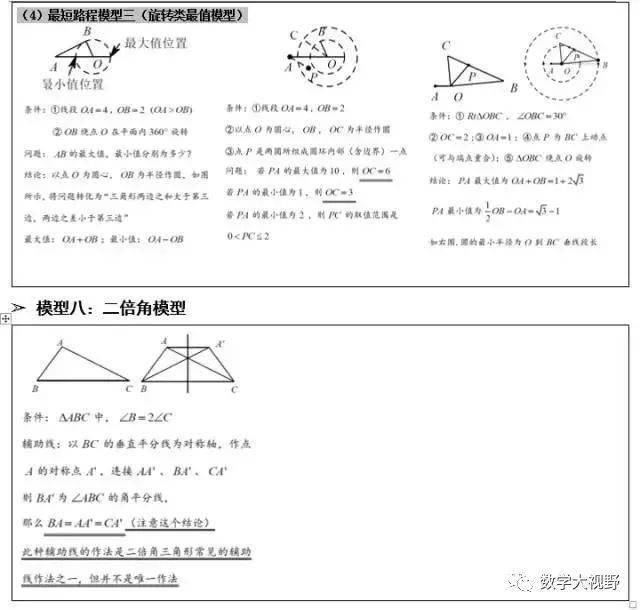
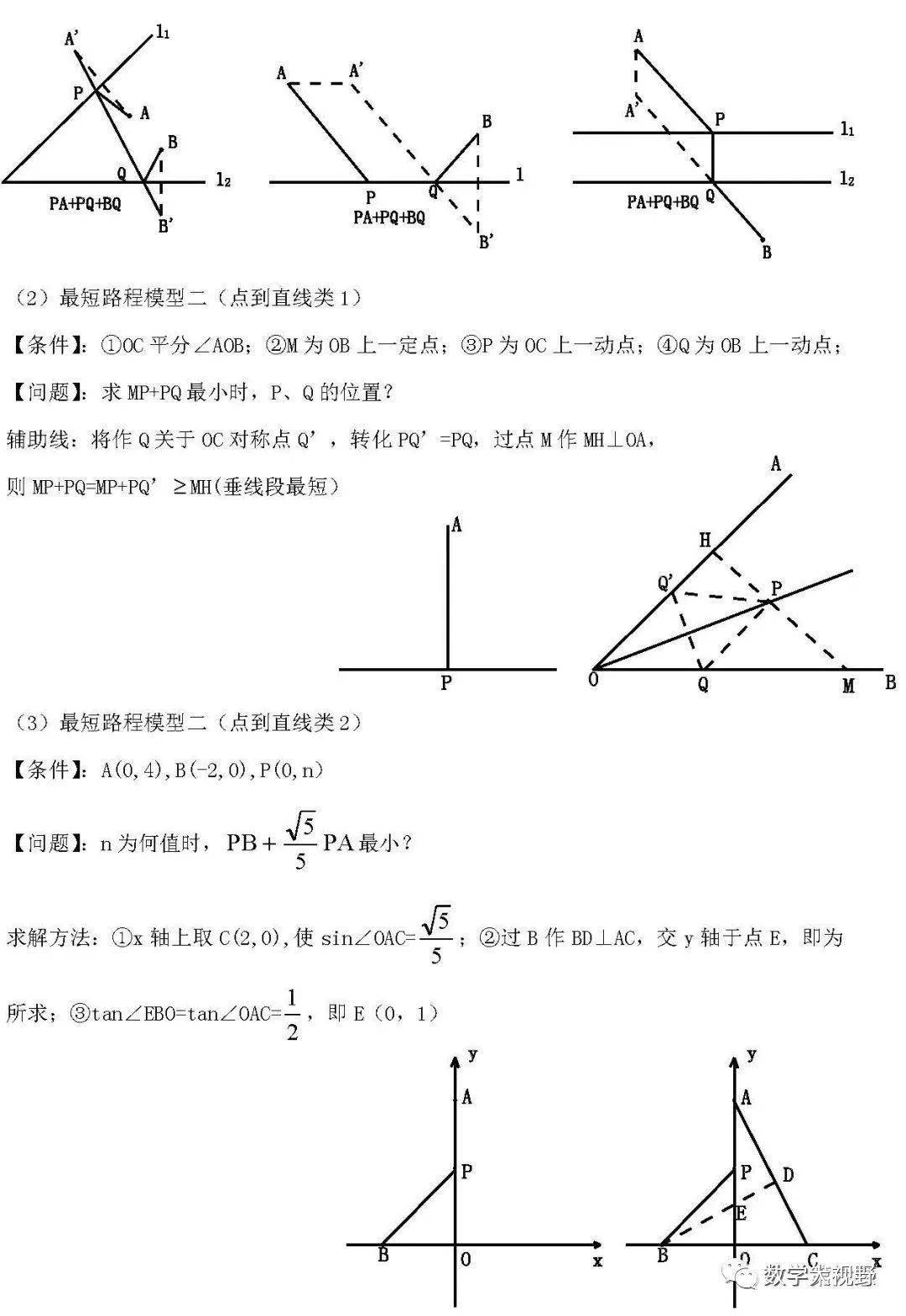
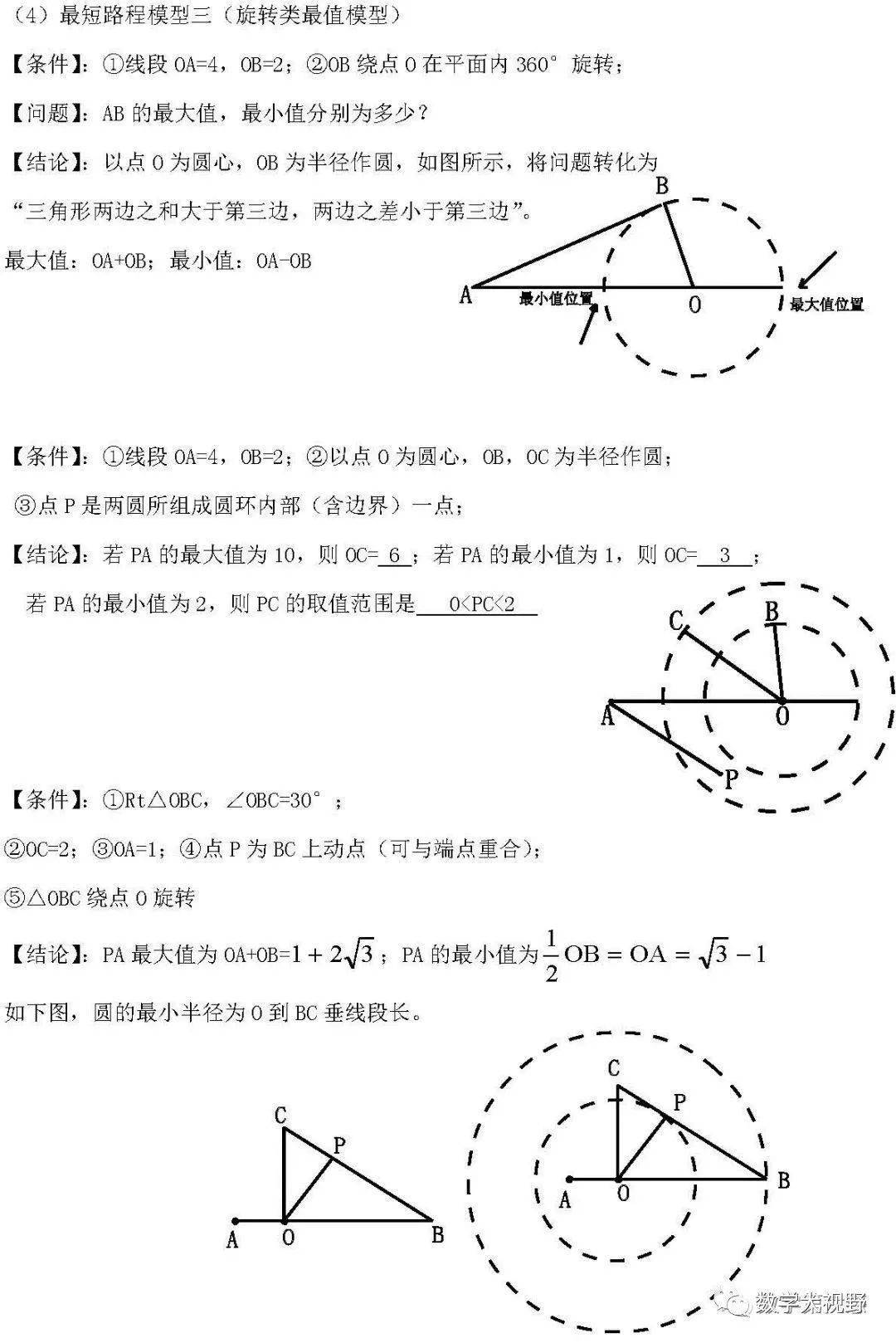
最短路径模型
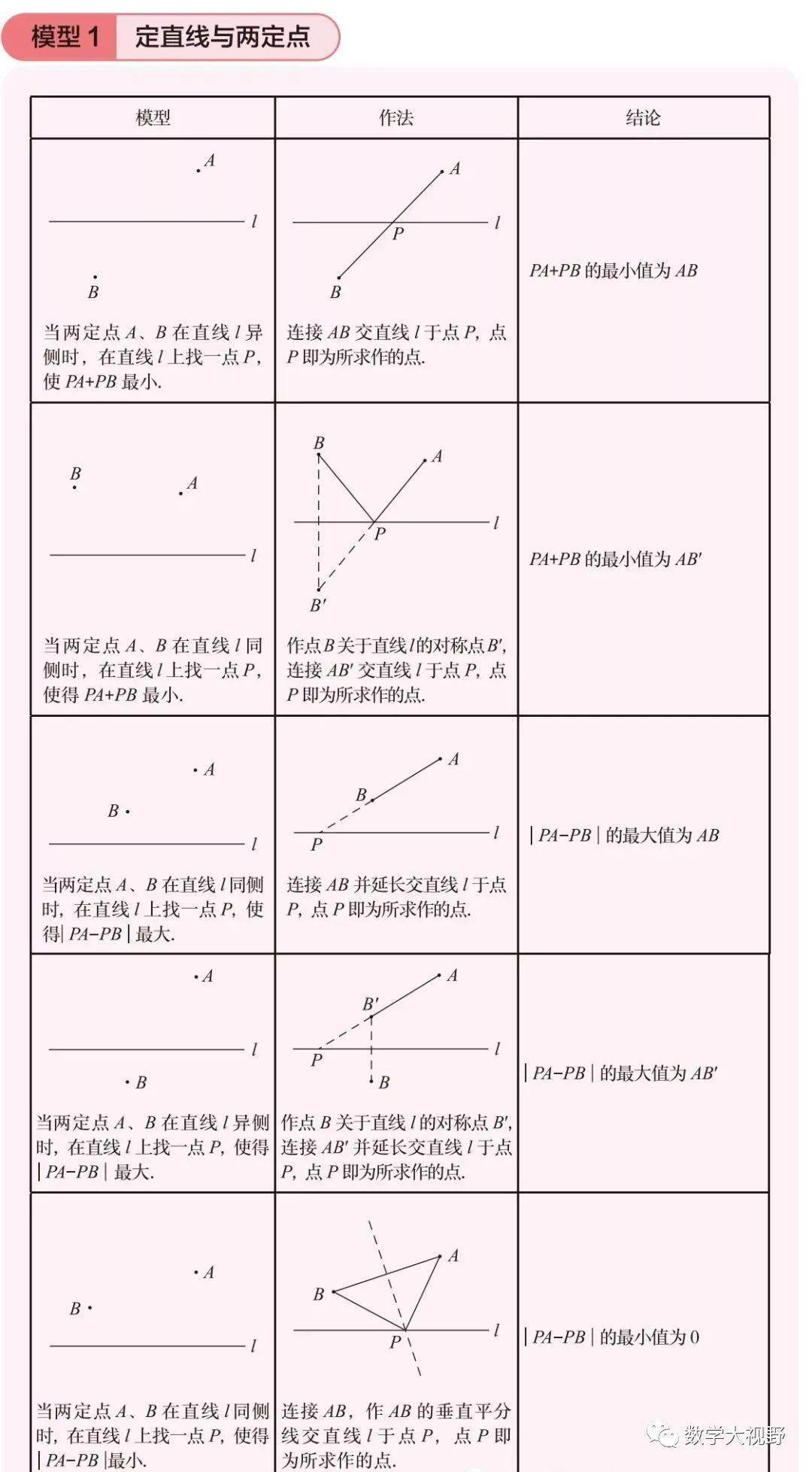
1、将军饮马【两点之间线段最短】
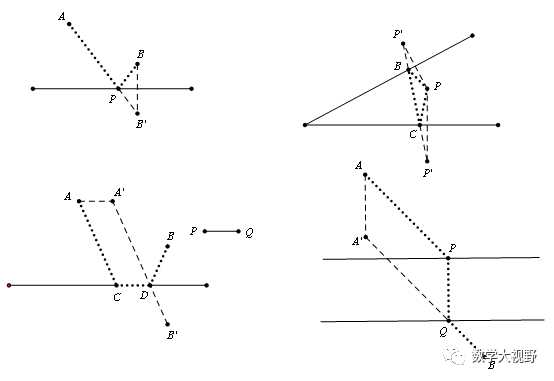
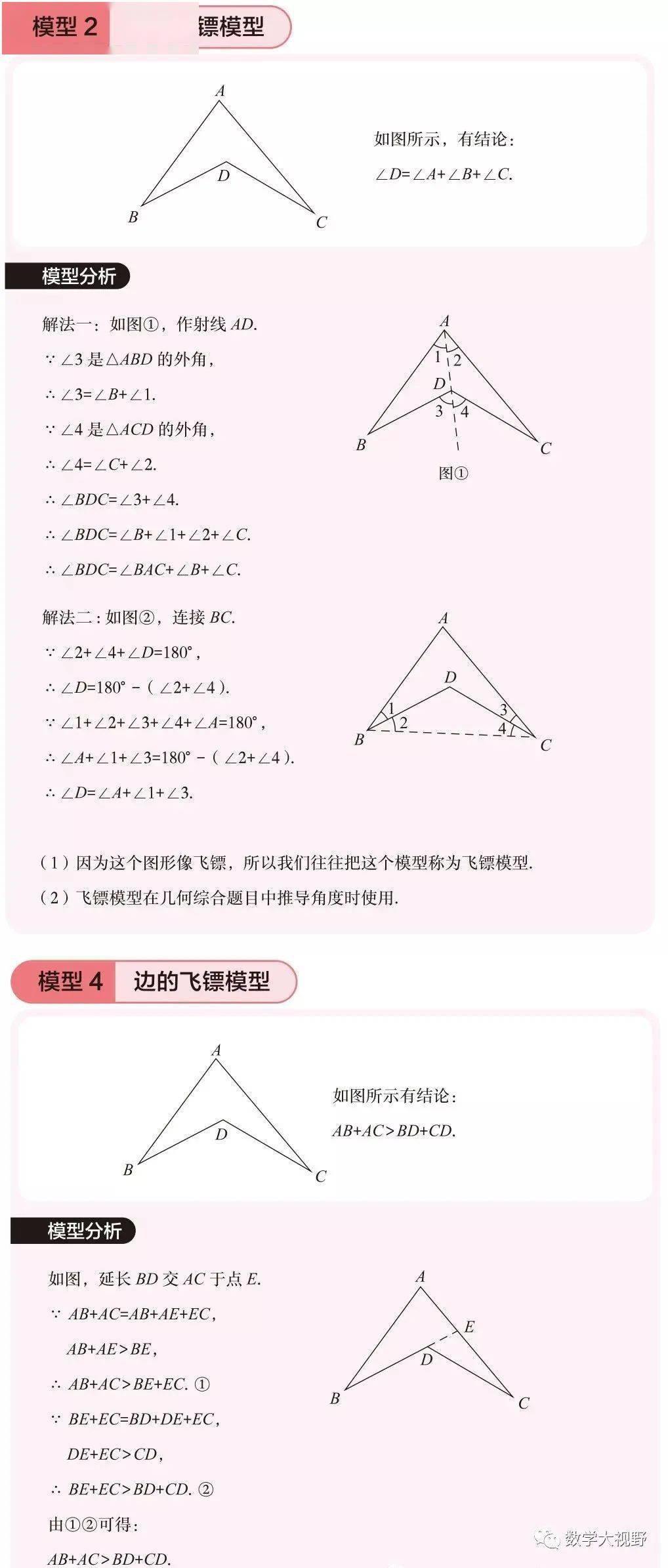
2、费马点【垂线段最短】
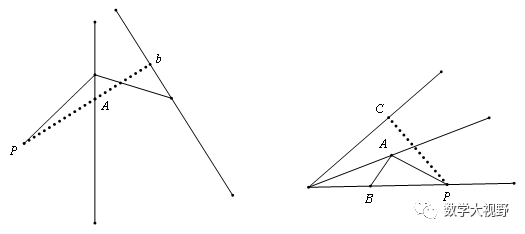
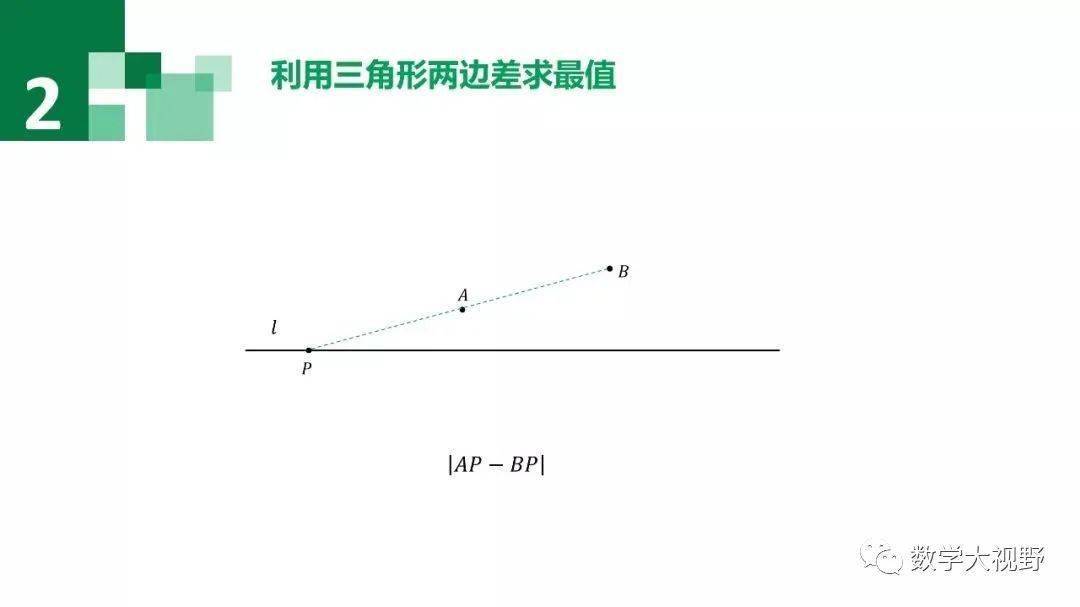
3、【两边之差小于第三边】
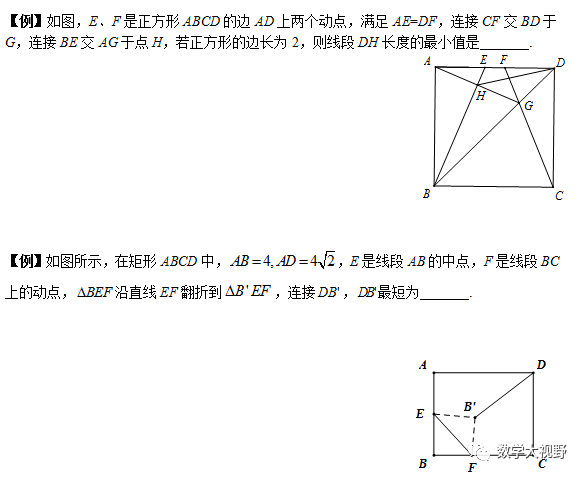
NO.3
【初中数学模型解题法(经典)】
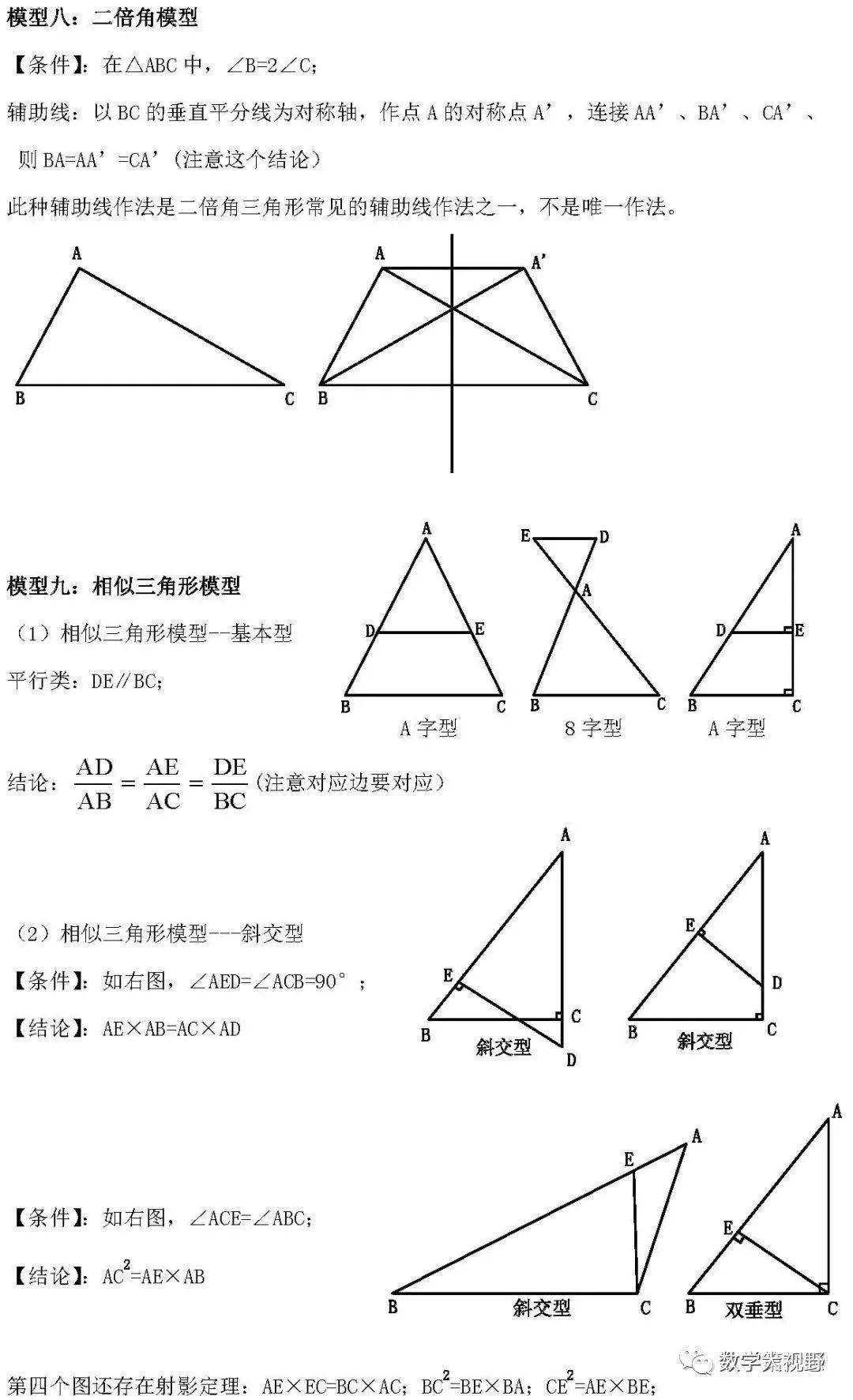
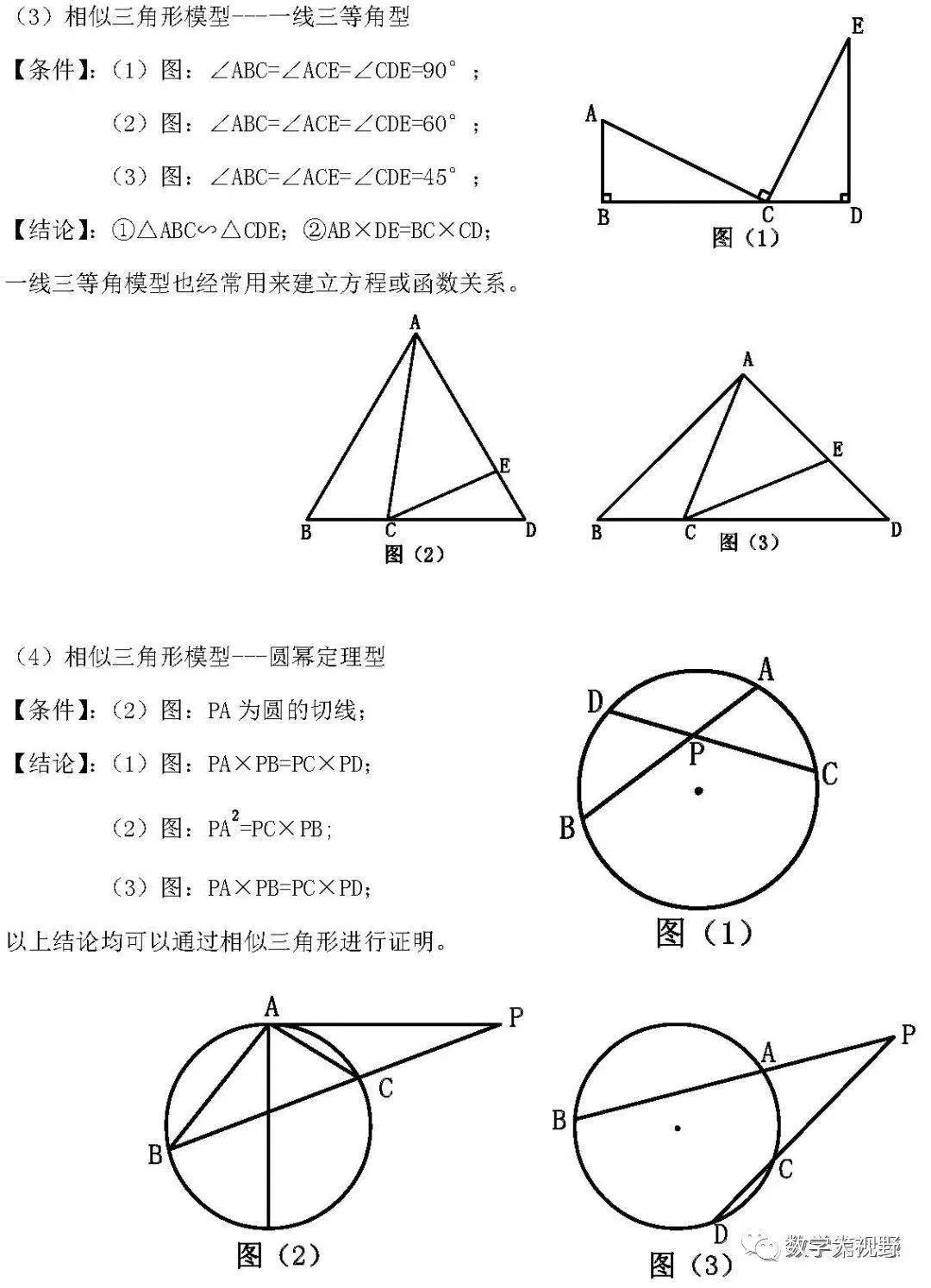
NO.4
【最值模型将军饮马、将军遛马、将军过河】
白日登山望烽火,黄昏饮马傍交河。——唐代·李颀《古从军行》
01
什么是将军饮马?
【问题描述】
如图,将军在图中点A处,现在他要带马去河边喝水,之后返回军营,问:将军怎么走能使得路程最短?

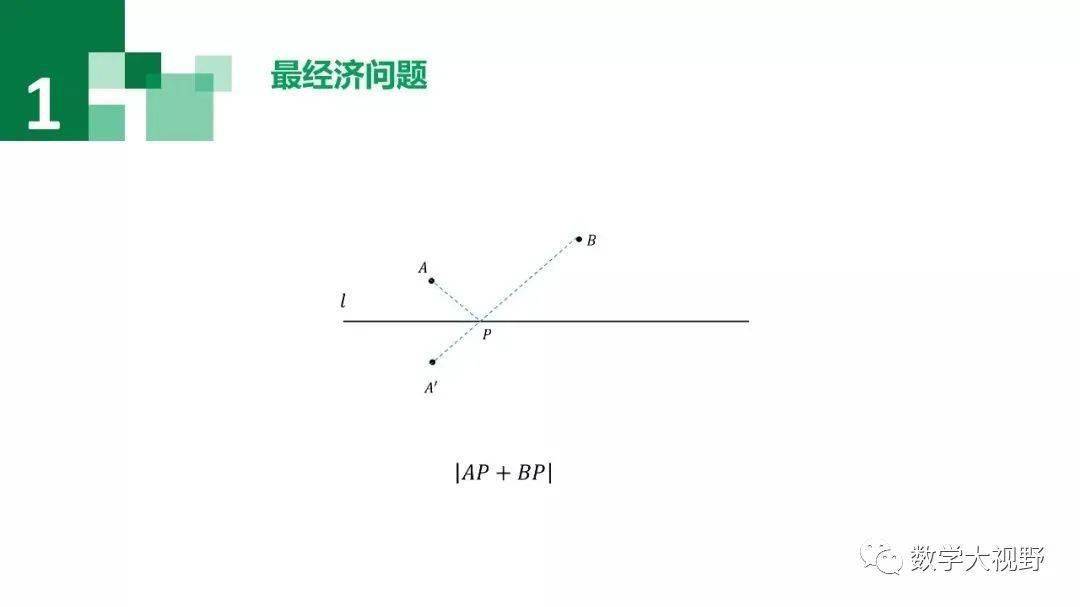
【问题简化】
如图,在直线上找一点P使得PA+PB最小?

【问题分析】
这个问题的难点在于PA+PB是一段折线段,通过观察图形很难得出结果,关于最小值,我们知道“两点之间,线段最短”、“点到直线的连线中,垂线段最短”等,所以此处,需转化问题,将折线段变为直线段.
【问题解决】
作点A关于直线的对称点A',连接PA',则PA'=PA,所以PA+PB=PA'+PB

当A'、P、B三点共线的时候,PA'+PB=A'B,此时为最小值(两点之间线段最短)
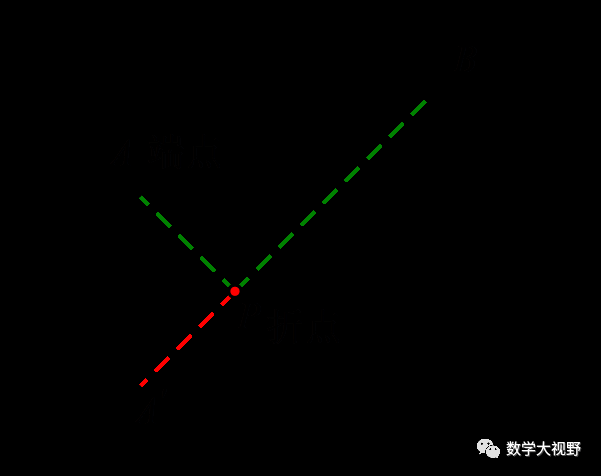
作端点(点A或点B)关于折点(上图P点)所在直线的对称,化折线段为直线段.
02
将军饮马模型系列
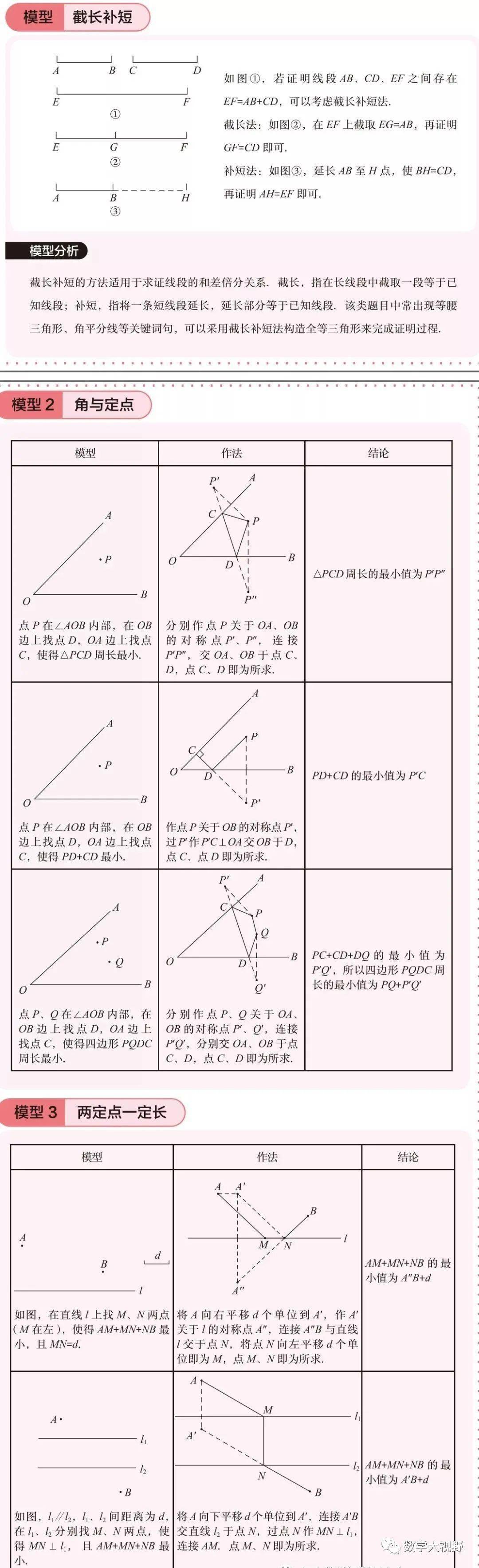
“一定两动”之点到点
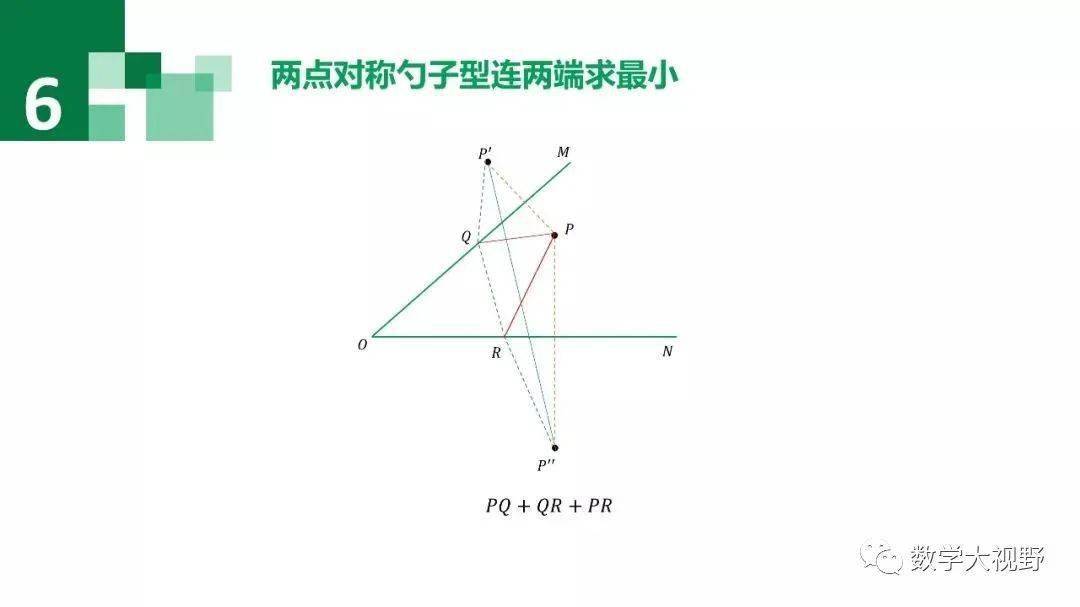
在OA、OB上分别取点M、N,使得△PMN周长最小。
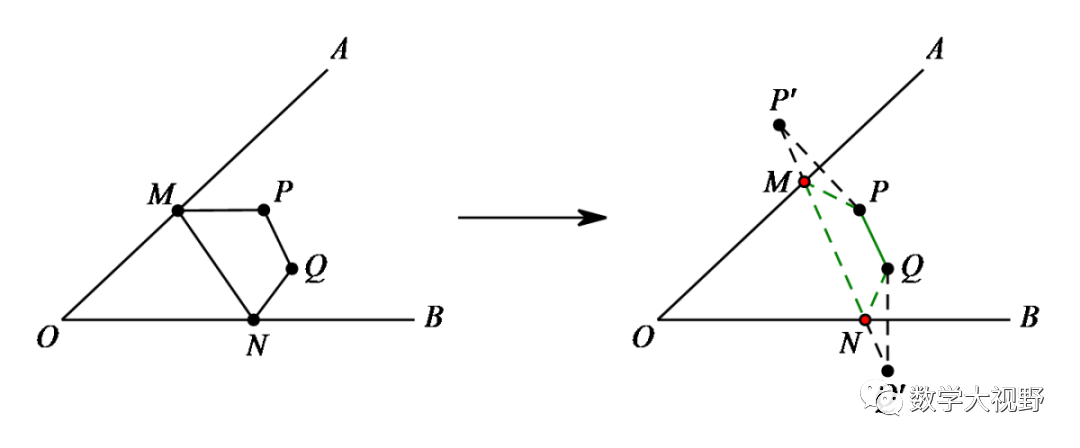
此处M、N均为折点,分别作点P关于OA(折点M所在直线)、OB(折点N所在直线)的对称点,化折线段PM+MN+NP为P'M+MN+NP'',当P'、M、N、P''共线时,△PMN周长最小。
························································
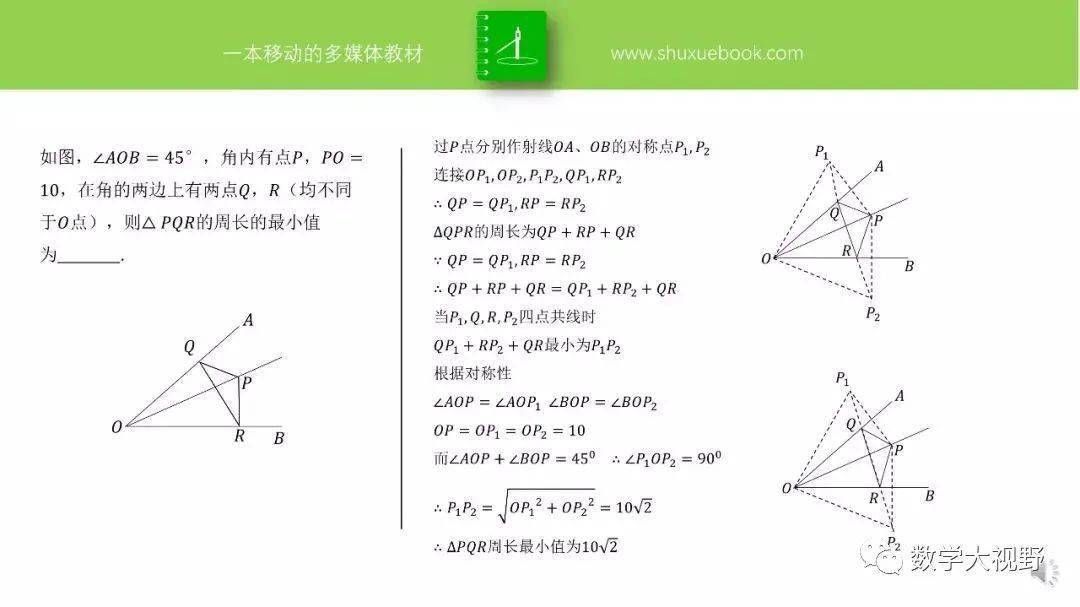
【例题】如图,点P是∠AOB内任意一点,∠AOB=30°,OP=8,点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值为________.

【分析】△PMN周长即PM+PN+MN的最小值,此处M、N均为折点,分别作点P关于OB、OA对称点P'、P'',化PM+PN+MN为P'N+MN+P''M.
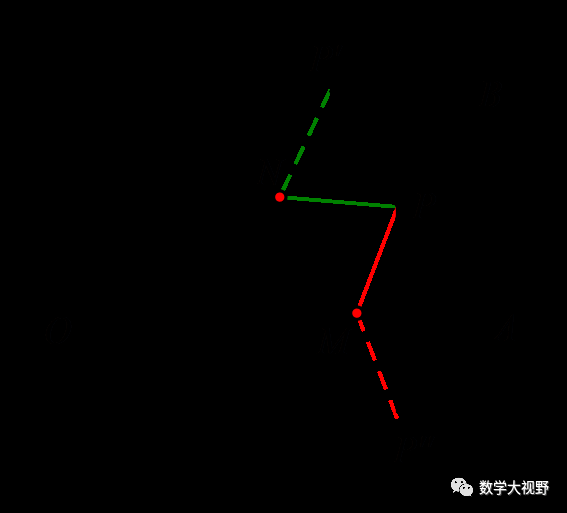
当P'、N、M、P''共线时,得△PMN周长的最小值,即线段P'P''长,连接OP'、OP'',可得△OP'P''为等边三角形,所以P'P''=OP'=OP=8.

“两定两动”之点到点
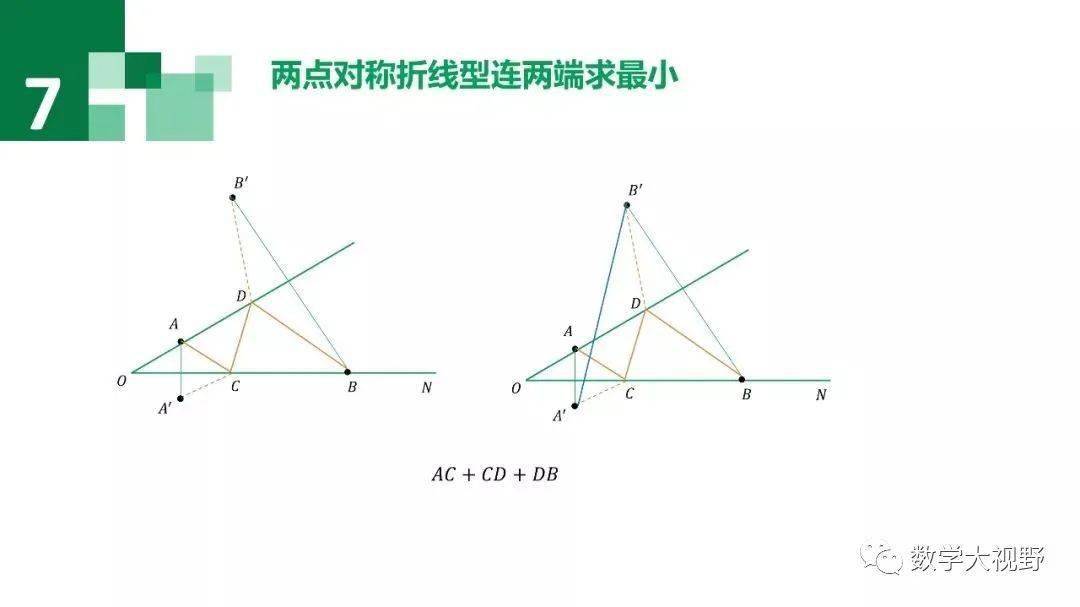
在OA、OB上分别取点M、N使得四边形PMNQ的周长最小。
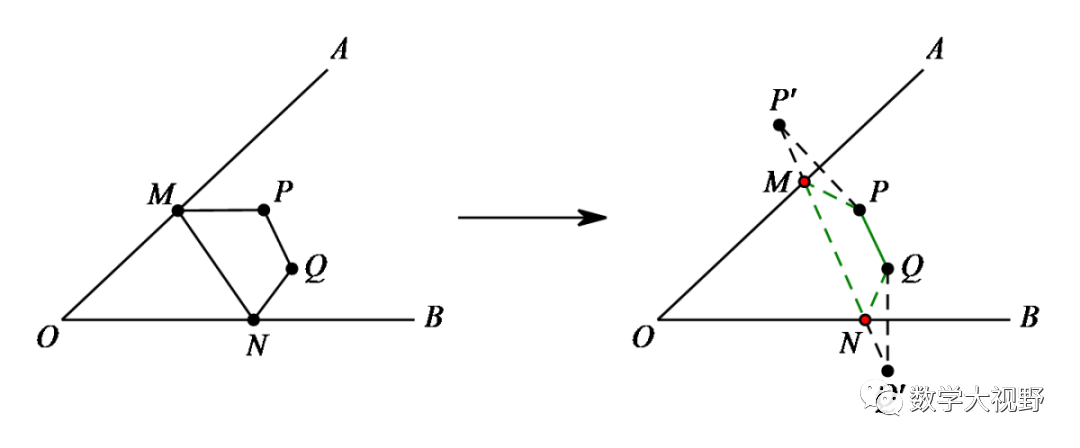
考虑PQ是条定线段,故只需考虑PM+MN+NQ最小值即可,分别作点P、Q关于OA、OB对称,化折线段PM+MN+NQ为P'M+MN+NQ',当P'、M、N、Q'共线时,四边形PMNQ的周长最小。
“一定两动”之点到线
在OA、OB上分别取M、N使得PM+MN最小。
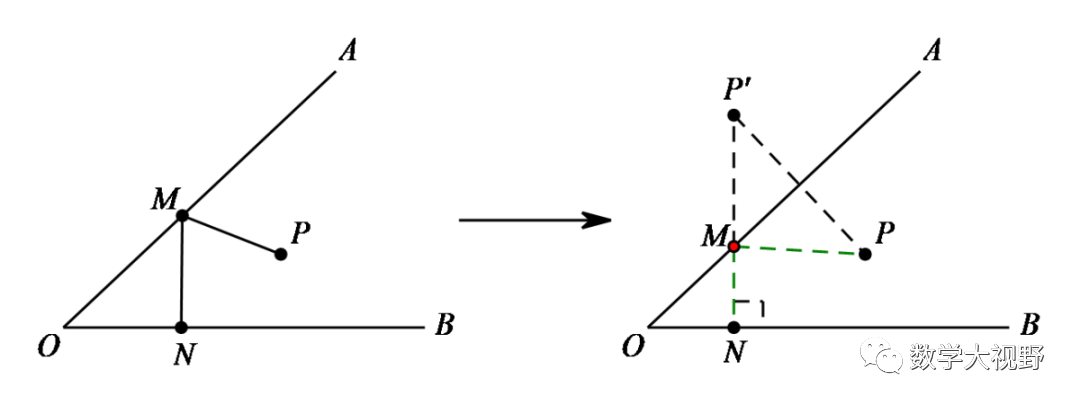
此处M点为折点,作点P关于OA对称的点P',将折线段PM+MN转化为P'M+MN,即过点P'作OB垂线分别交OA、OB于点M、N,得PM+MN最小值(点到直线的连线中,垂线段最短)
03
几何图形中的将军饮马
寻找几何图形中端点关于折点所在直线的对称点位置
正方形中的将军饮马
【关于对角线对称】
如图,正方形ABCD的边长是4,M在DC上,且DM=1, N是AC边上的一动点,则△DMN周长的最小值是________.

【分析】考虑DM为定值,故求△DMN周长最小值即求DN+MN最小值.点N为折点,作点D关于AC的对称点,即点B,连接BN交AC于点N,此时△DMN周长最小.
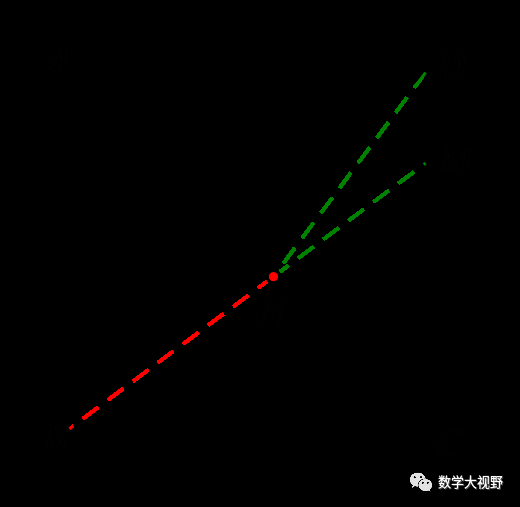
························································
【假装不存在的正方形】
(2019山东聊城)如图,在Rt△ABO中,∠OBA=90°,A(4,4),点C在边AB上,且AC:CB=1:3,点D为OB的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC周长最小的点P的坐标为( )

A.(2,2) B.(5/2,5/2)
C.(8/3,8/3) D.(3,3)
【分析】此处点P为折点,可以作点D关于折点P所在直线OA的对称:
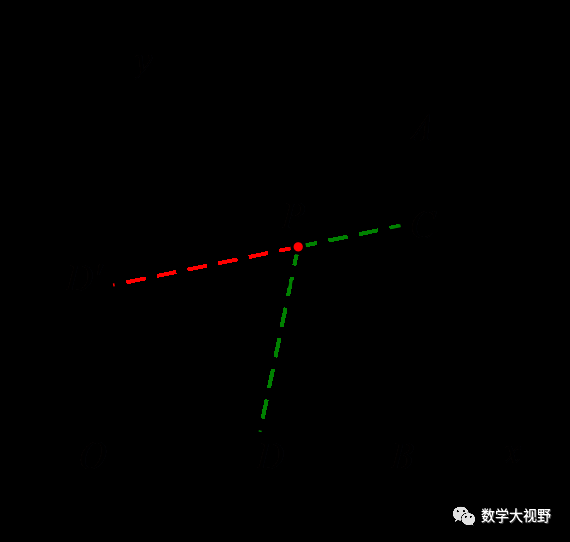
也可以作点C的对称:
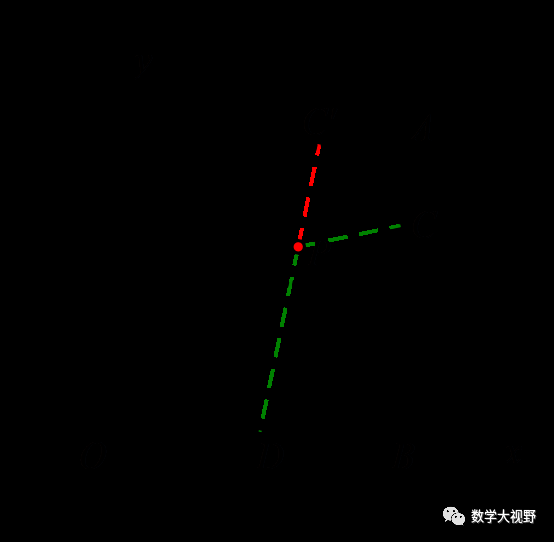
························································
【隐身的正方形】
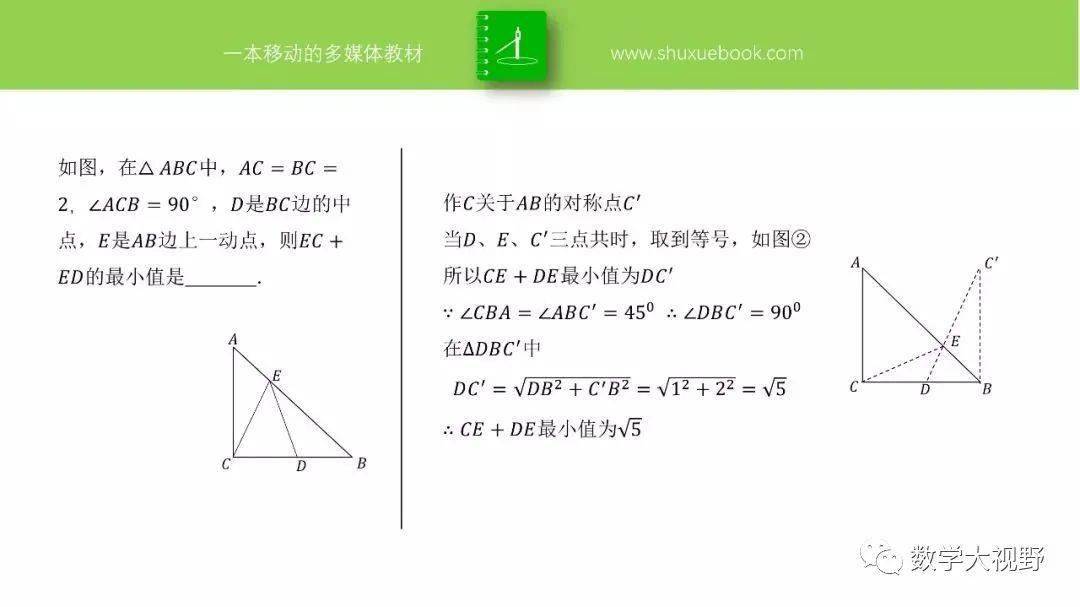
(2017辽宁营口)如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=3,DC=1,点P是AB上的动点,则PC+PD的最小值为( )

A.4 B.5 C.6 D.7
【分析】作点C关于P点所在直线AB的对称点C',当C'、P、D共线时,PC+PD最小,最小值为5,故选B.
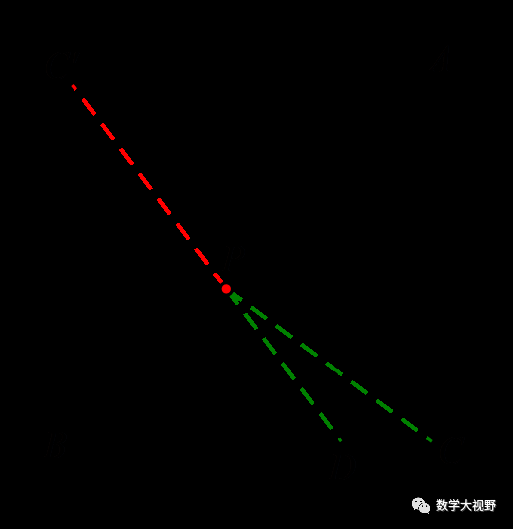
三角形中的将军饮马
【等边系列】
如图,在等边△ABC中,AB=6, N为AB上一点且BN=2AN, BC的高线AD交BC于点D,M是AD上的动点,连结BM,MN,则BM+MN的最小值是___________.

【分析】M点为折点,作B点关于AD的对称点,即C点,连接CN,即为所求的最小值.
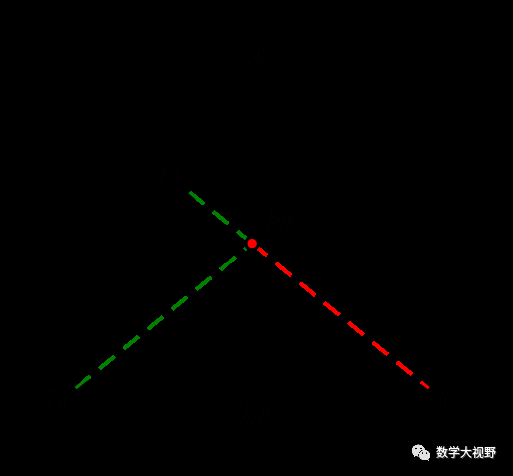
过点C作AB垂线,利用勾股定理求得CN的长为2倍根号7.

························································
【隐身的等边三角形】
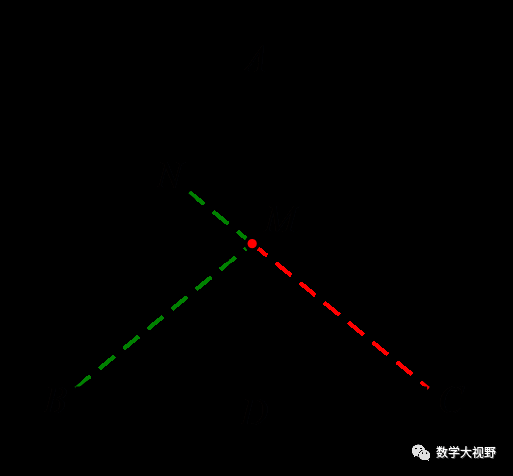
如图,在Rt△ABD中,AB=6,∠BAD=30°,∠D=90°,N为AB上一点且BN=2AN, M是AD上的动点,连结BM,MN,则BM+MN的最小值是________.

【分析】对称点并不一定总是在已知图形上.
························································
【角分线系列之点到点】
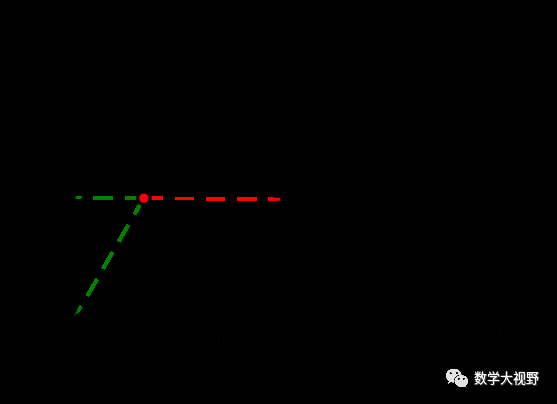
(2018山东潍坊)如图,在Rt△ABC中,∠ACB=90°,AC=6.AB=12,AD平分∠ACB,点F是AC的中点,点E是AD上的动点,则CE+EF的最小值为________.

【分析】此处E点为折点,可作点C关于AD的对称,对称点C'在AB上且在AB中点,化折线段CE+EF为C'E+EF,当C'、E、F共线时得最小值,C'E为CB的一半.
························································
【角分线系列之点到线】
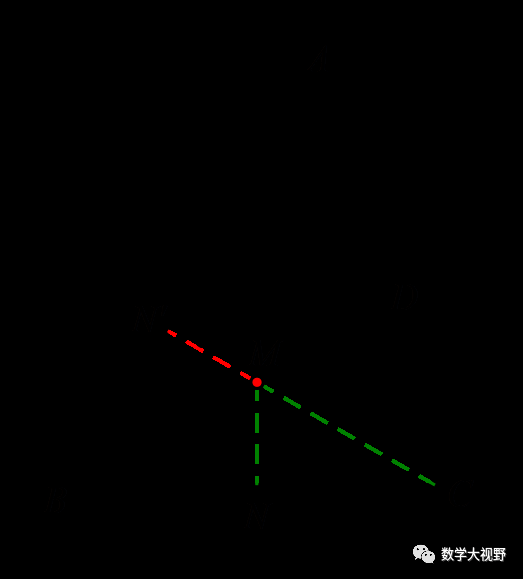
(2018辽宁营口)如图,在锐角三角形ABC中,BC=4,∠ABC=60°, BD平分∠ABC,交AC于点D,M、N分别是BD,BC上的动点,则CM+MN的最小值是________.

【分析】此处M点为折点,作点N关于BD的对称点,恰好在AB上,化折线CM+MN为CM+MN'.

因为M、N皆为动点,所以过点C作AB的垂线,可得最小值.
菱形、矩形中的将军饮马
【菱形高】
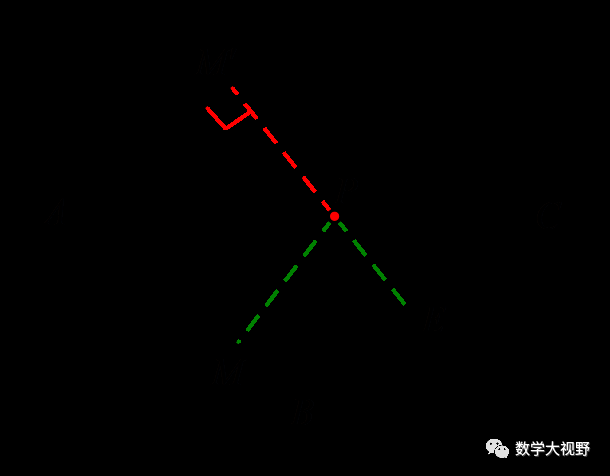
(2018广西贵港)如图,在菱形ABCD中,AC为6倍根号2,BD=6,E是BC的中点,P、M分别是AC、AB上的动点,连接PE、PM,则PE+PM的最小值是____________.

【分析】此处P为折点,作点M关于AC的对称点M',恰好在AD上,化折线EP+PM为EP+PM'.

当E、P、M'共线时,EP+PM最小,最小值即为菱形的高,可用面积法:AC·BD=BC·EM'.
························································
【折点在边上】
(2017山东菏泽)如图,矩形ABOC的顶点A的坐标为(-4,5),D是OB的中点,E是OC上的一点,当△ADE的周长最小时,点E的坐标是__________.

【分析】点E为折点,E是y轴上一点,作点D关于y轴的对称点D',连接AD,与y轴交点即为所求E点.

························································
【面积与折点】
(2019西藏)如图,在矩形ABCD中,AB=6,AD=3,动点P满足△APB的面积是矩形ABCD面积的三分之一,则点P到A、B两点距离之和PA+PB的最小值为_________.

【分析】由△APB面积是矩形面积三分之一,可作出P点轨迹为直线MN(AM=BN=2),作点B关于MN的对称点B',化折线PA+PB为PA+PB'.
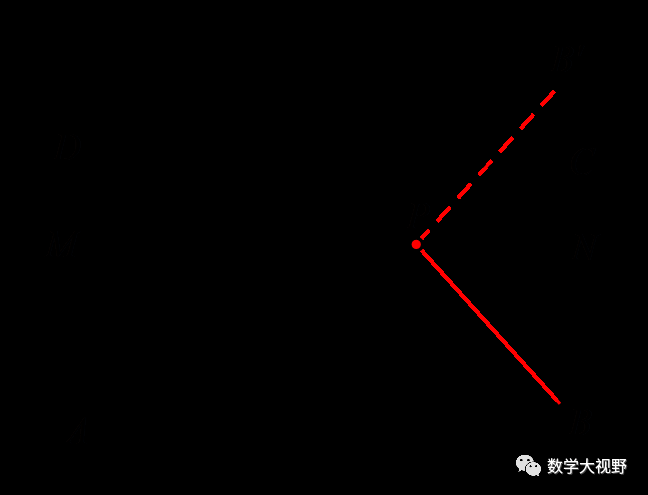
当A、P、B'共线时,取到最小值.
························································
【全等与对称】
(2017江苏南通)如图,矩形ABCD中,AB=10,BC=5,点E、F、G、H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为________.

【分析】考虑到四边形EFGH是平行四边形,即求EH+EF最小值,此处E为折点,作F关于AB对称点F',则BF'=BF=DH=CM,∴MF'=BC=5,MH=DC=10,∴HF'为5倍根号5,周长最小值为10倍根号5.
04
特殊角的对称
60°角的对称
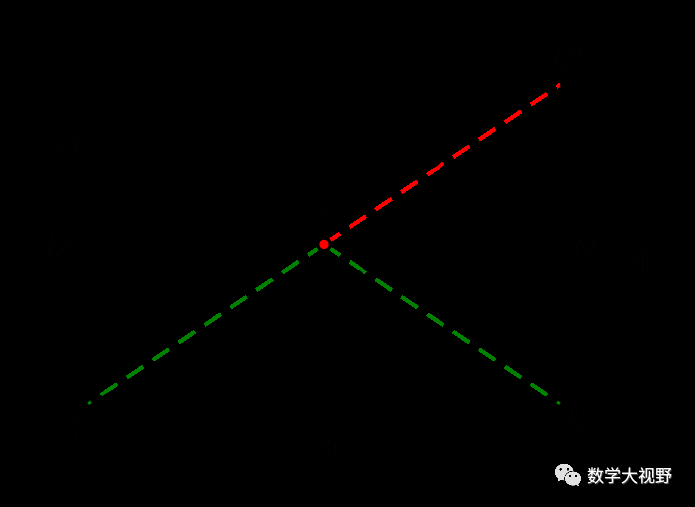
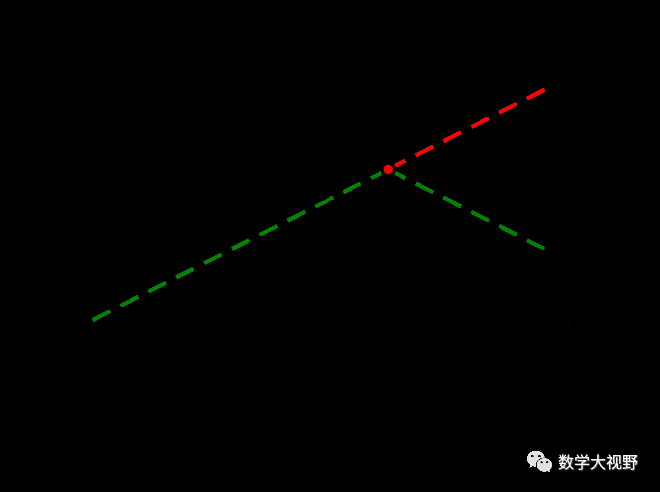
(2018滨州)如图,∠AOB=60°,点P是∠AOB内的定点且OP为根号3,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是_________.

【分析】此处M、N均为折点,分别作点P关于OB、OA的对称点P'、P'',化△PMN周长为P'N+NM+MP''.
当P'、N、M、P''共线时,得最小值,利用60°角翻倍得∠P'OP''=120°,OP'=OP''=OP,可得最小值.
30°角的对称
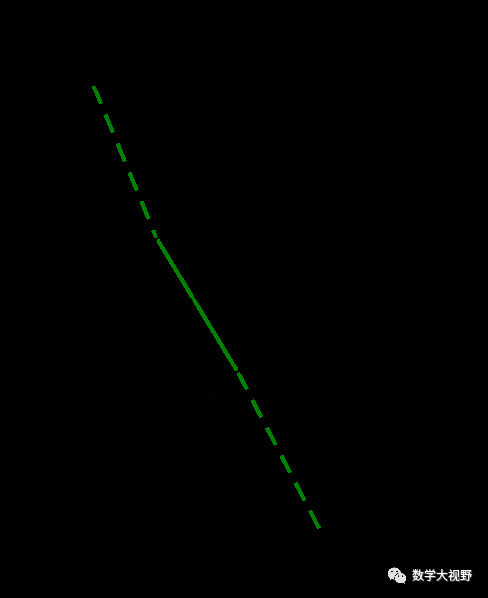
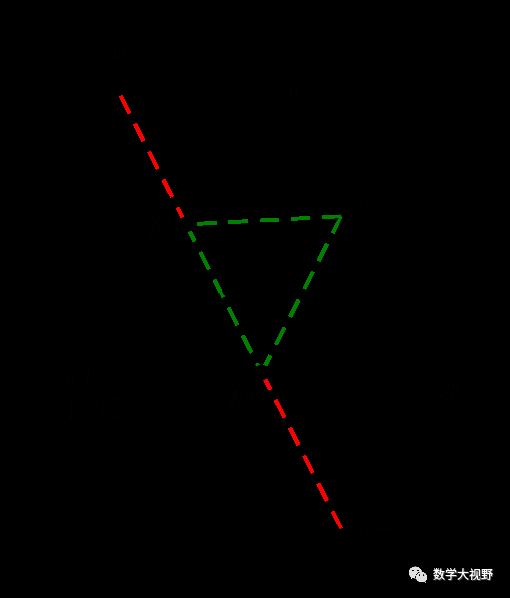
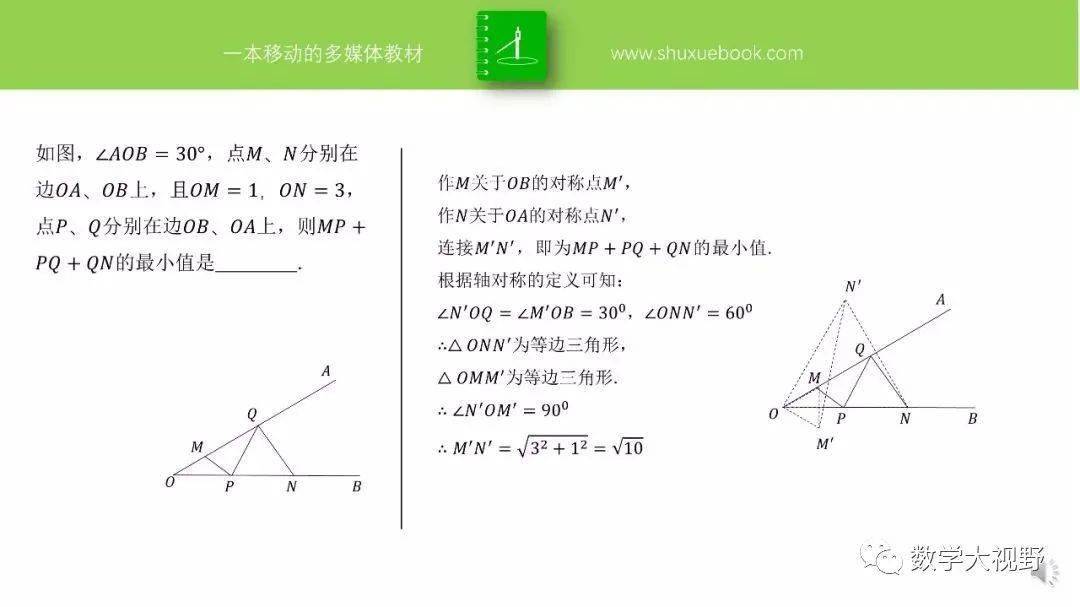
(2017湖北随州)如图,∠AOB的边OB与x轴正半轴重合,点P是OA上的一动点,点N(3,0)是OB上的一定点,点M是ON的中点,∠AOB=30°,要使PM+PN最小,则点P的坐标为_________.

【分析】此处点P为折点,作点M关于OA的对称对称点M'如图所示,连接PM',化PM+PN为PM'+PN.

当M'、P、N共线时,得最小值,又∠M'ON=60°且ON=2OM',可得∠OM'N=90°,故P点坐标可求.
20°角的对称
如图,已知正比例函数y=kx(k>0)的图像与x轴相交所成的锐角为70°,定点A的坐标为(0,4),P为y轴上的一个动点,M、N为函数y=kx(k>0)的图像上的两个动点,则AM+MP+PN的最小值为____________.

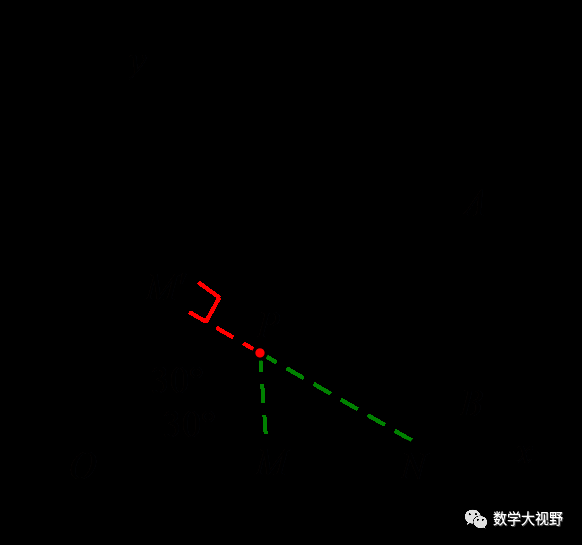
【分析】先考虑M为折点,作点P关于OM对称点P',化AM+MP+PN为AM+MP'+P'N
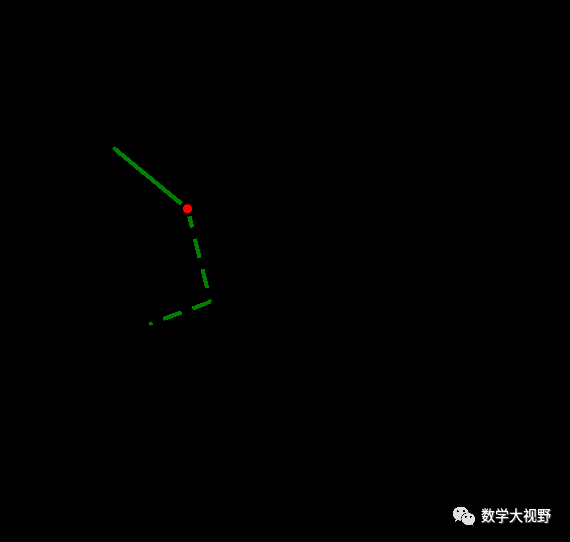
此处P'为折点,作点N关于OP'对称点N',化AM+MP'+P'N为AM+MP'+P'N'

当A、M、P'、N'共线且AN'⊥ON'时,值最小.

05
将军过桥
已知将军在图中点A处,现要过河去往B点的军营,桥必须垂直于河岸建造,问:桥建在何处能使路程最短?

【分析】考虑MN长度恒定,只要求AM+NB最小值即可.问题在于AM、NB彼此分离,所以首先通过平移,使AM与NB连在一起,将AM向下平移使得M、N重合,此时A点落在A'位置.
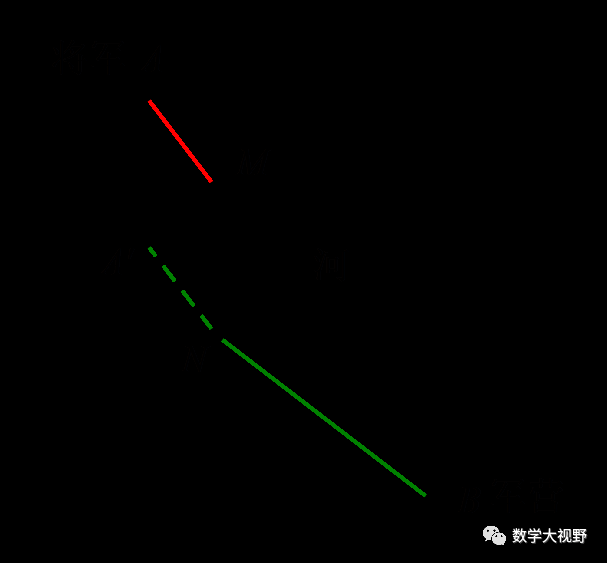
问题化为求A'N+NB最小值,显然,当共线时,值最小,并得出桥应建的位置.

通过几何变换将若干段原本彼此分离线段组合到一起,是解决问题的关键~
将军过双桥
已知将军在图中点A处,现要过两条河去往B点的军营,桥必须垂直于河岸建造,问:桥建在何处能使路程最短?
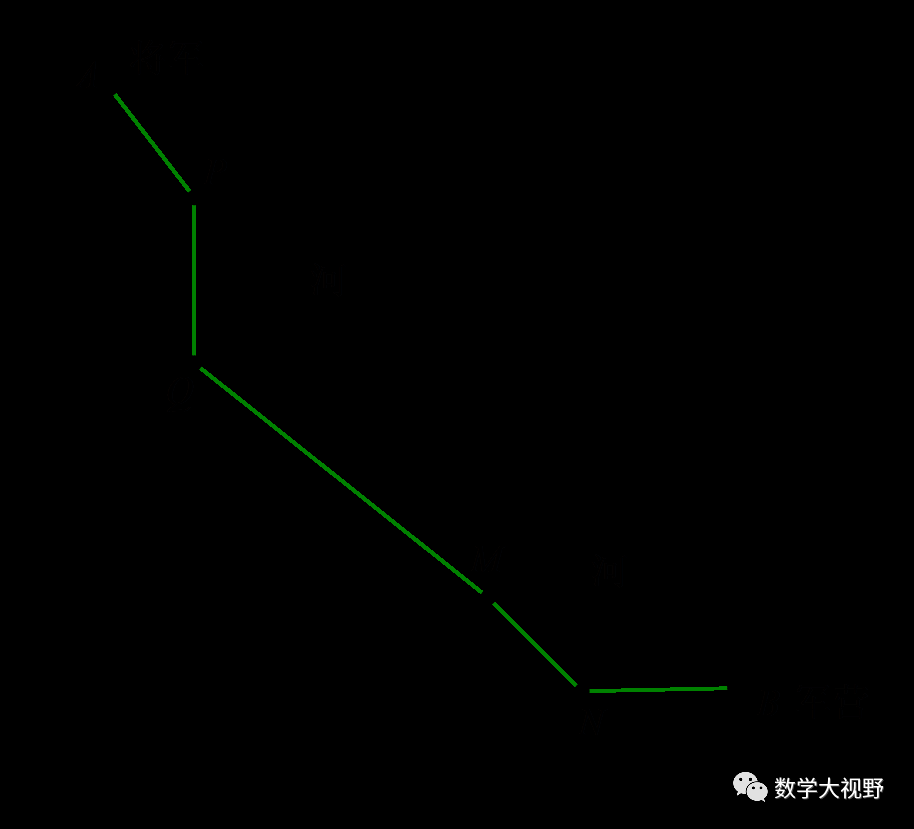
【分析】考虑PQ、MN均为定值,所以路程最短等价于AP+QM+NB最小,对于这彼此分离的三段,可以通过平移使其连接到一起.AP平移至A'Q,NB平移至MB',化AP+QM+NB为A'Q+QM+MB'.

当A'、Q、M、B'共线时,A'Q+QM+MB'取到最小值,再依次确定P、N位置.
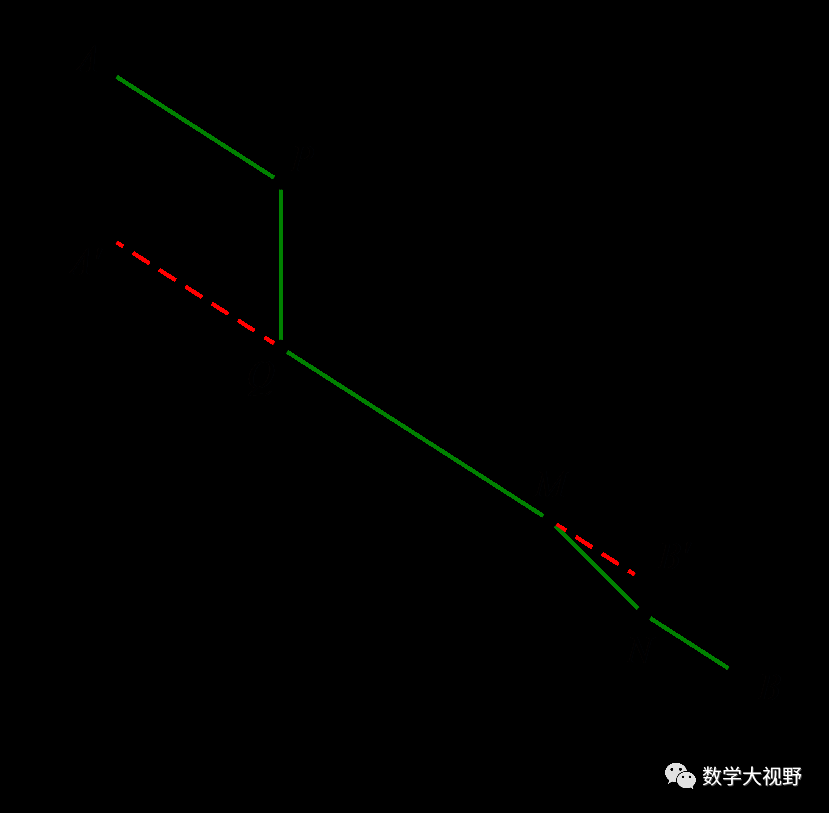
去除定量,组合变量
06
将军遛马
【问题介绍】
如图,将军在A点处,现在将军要带马去河边喝水,并沿着河岸走一段路,再返回军营,问怎么走路程最短?
【模型简化】
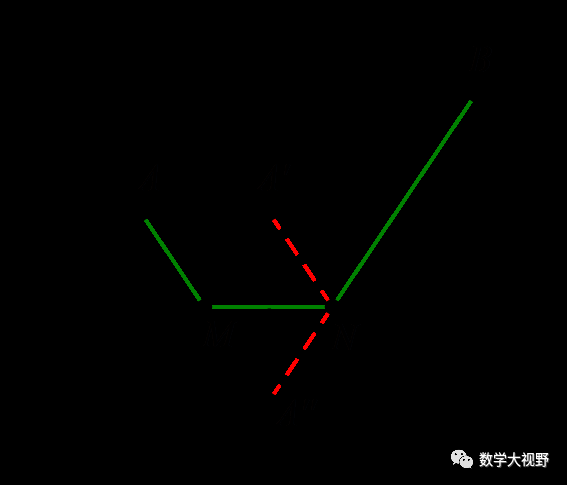
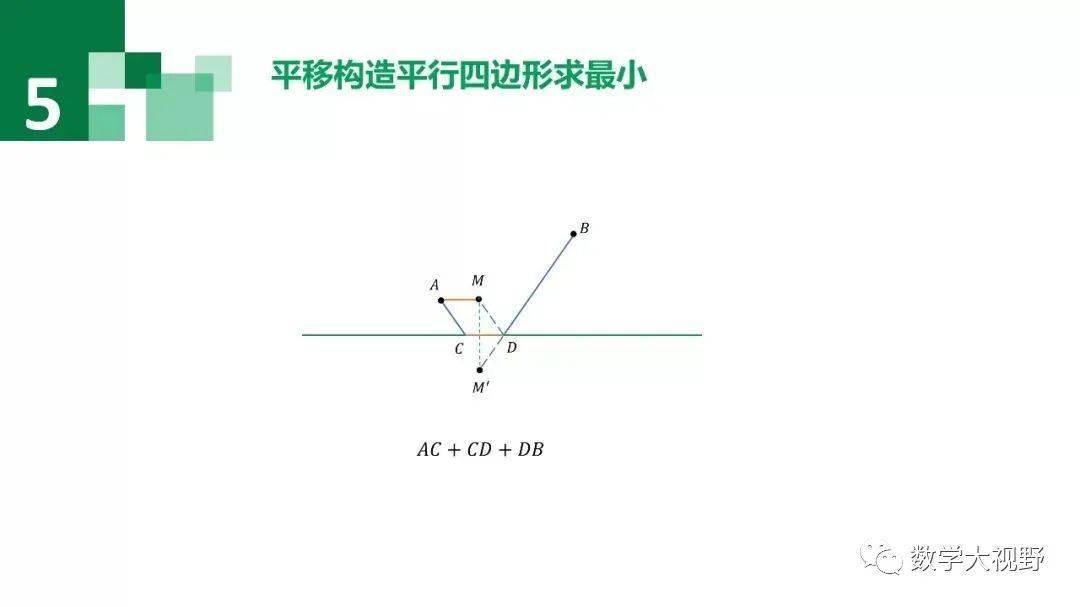
已知A、B两点,MN长度为定值,求确定M、N位置使得AM+MN+NB值最小?

【分析】考虑MN为定值,故只要AM+BN值最小即可.将AM平移使M、N重合,AM=A'N,将AM+BN转化为A'N+NB.

构造点A关于MN的对称点A'',连接A''B,可依次确定N、M位置,可得路线.
一个例子
如图,在平面直角坐标系中,矩形ABCD的顶点B在原点,点A、C在坐标轴上,点D的坐标为(6,4),E为CD的中点,点P、Q为BC边上两个动点,且PQ=2,要使四边形APQE的周长最小,则点P的坐标为________.

【分析】考虑PQ、AE为定值,故只要AP+QE最小即可,如图,将AP平移至A'Q,考虑A'Q+QE最小值.

作点A'关于x轴的对称点A'',连接A''E,与x轴交点即为Q点,左移2个单位即得P点.
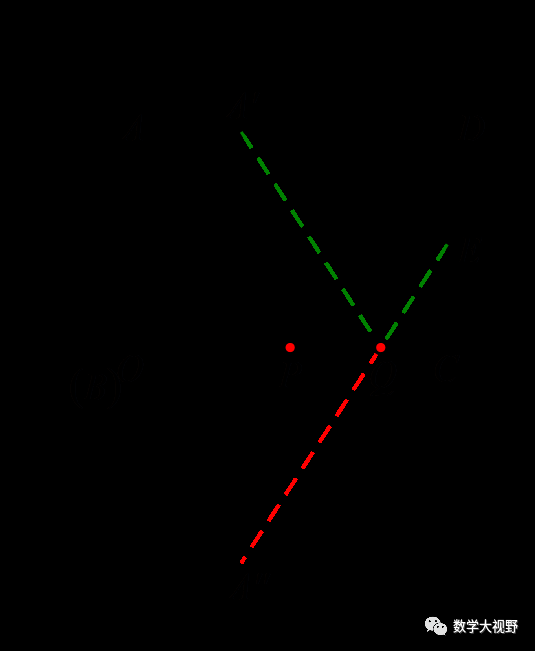
挖掘定量
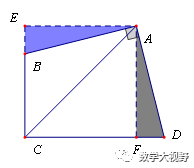
如图,矩形ABCD中,AD=2,AB=4,AC为对角线,E、F分别为边AB、CD上的动点,且EF⊥AC于点M,连接AF、CE,求AF+CE的最小值.

【分析】此题难点在于要得到AF与CE之间的关系,方能将这两条线段联系到一起.过点E作EH⊥CD交CD于H点,由相似可得:FH=1.
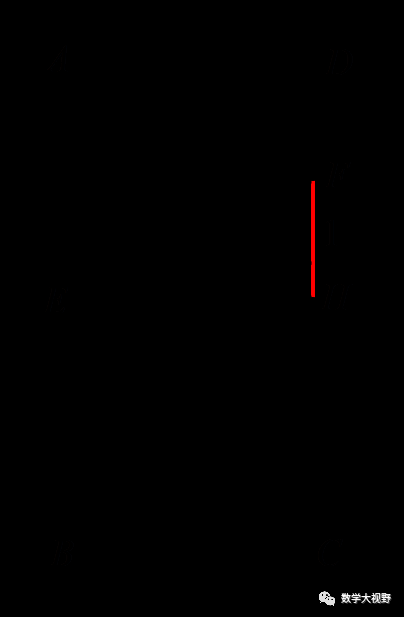
连接BH,则BH=CE

问题转化为BH+AF最小值.
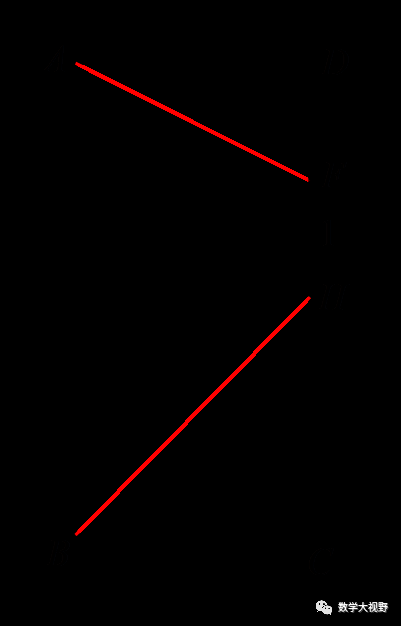
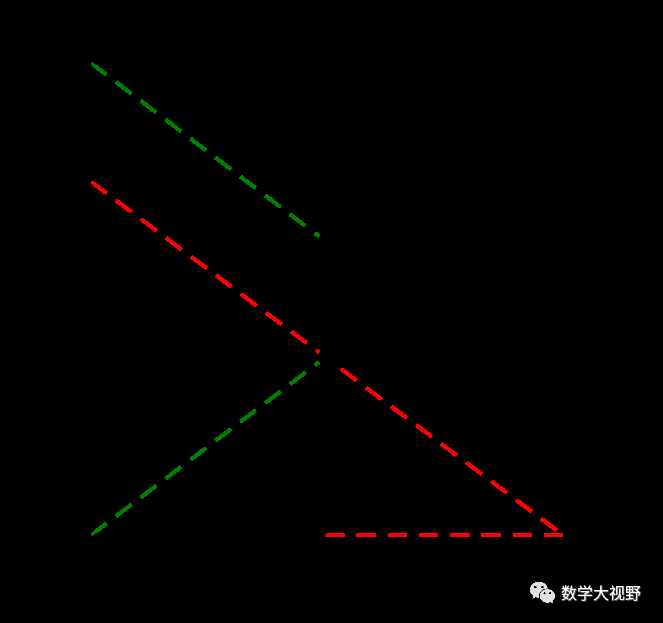
参考将军遛马的作法,作出图形,得出AF+BH=A'H+B'H=A'B'=5.
NO.5
【动点 最值问题19大模型(经典)】
温馨提示:点击图片,可查看大图








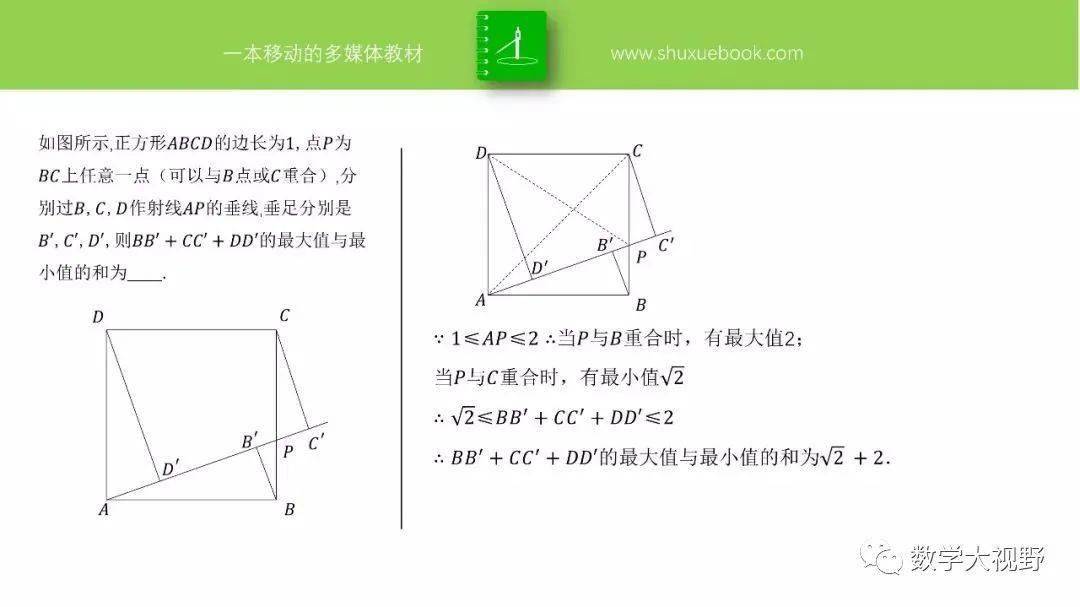

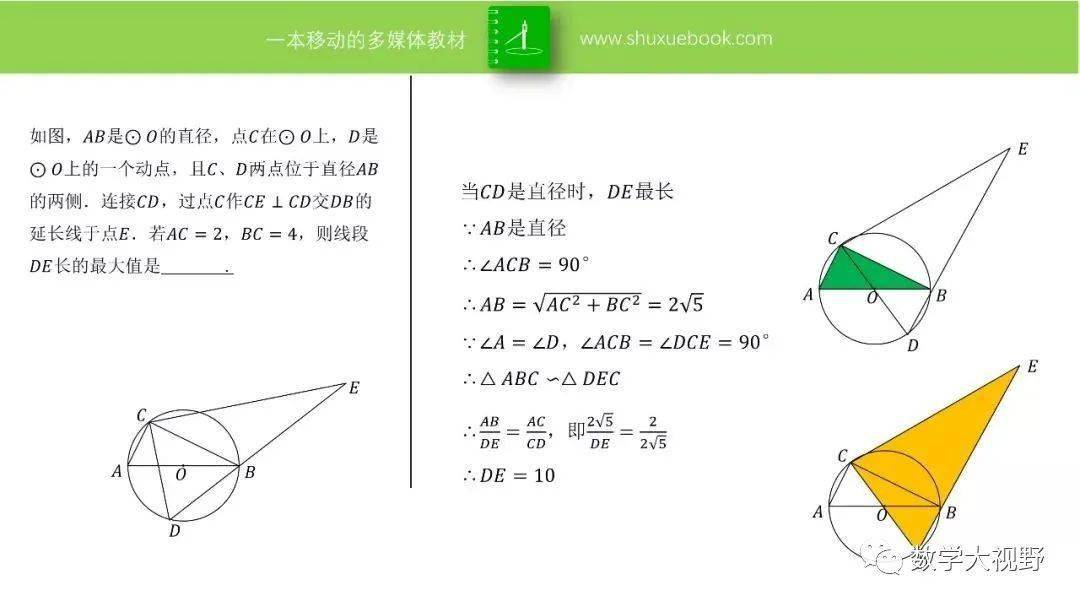





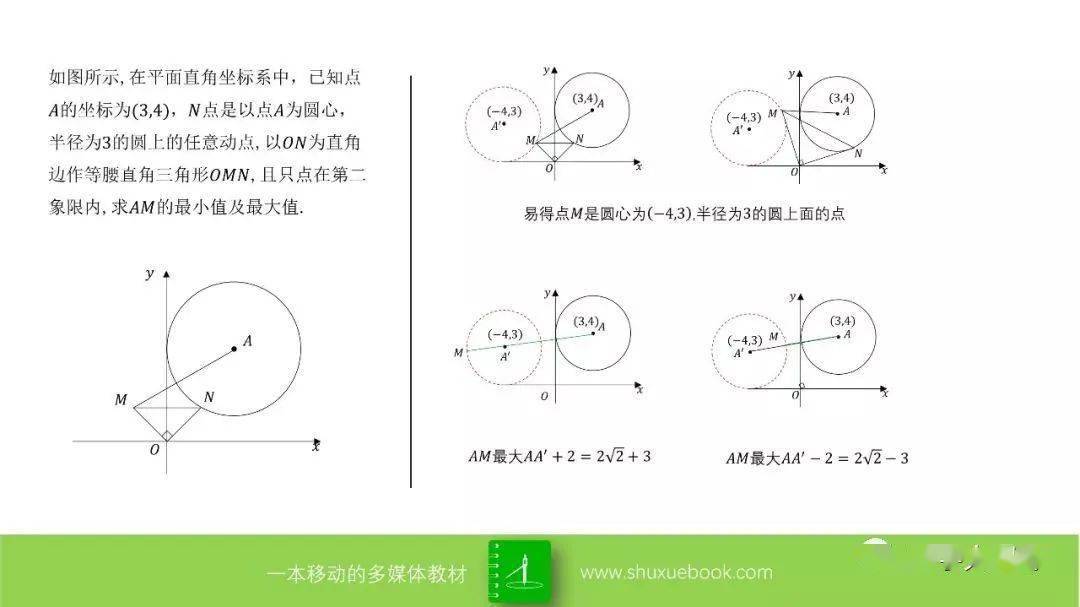

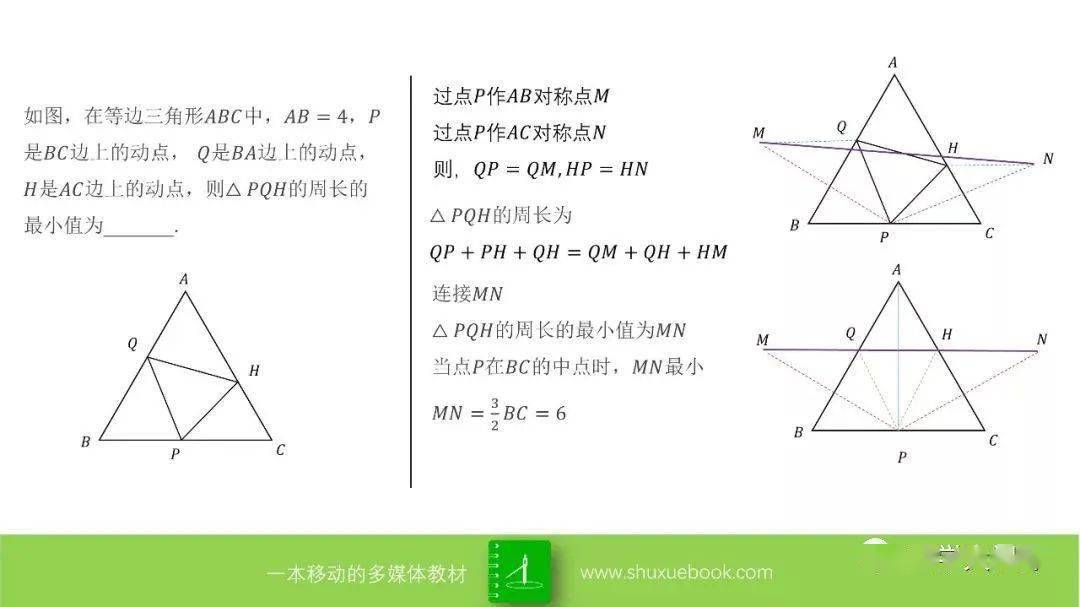



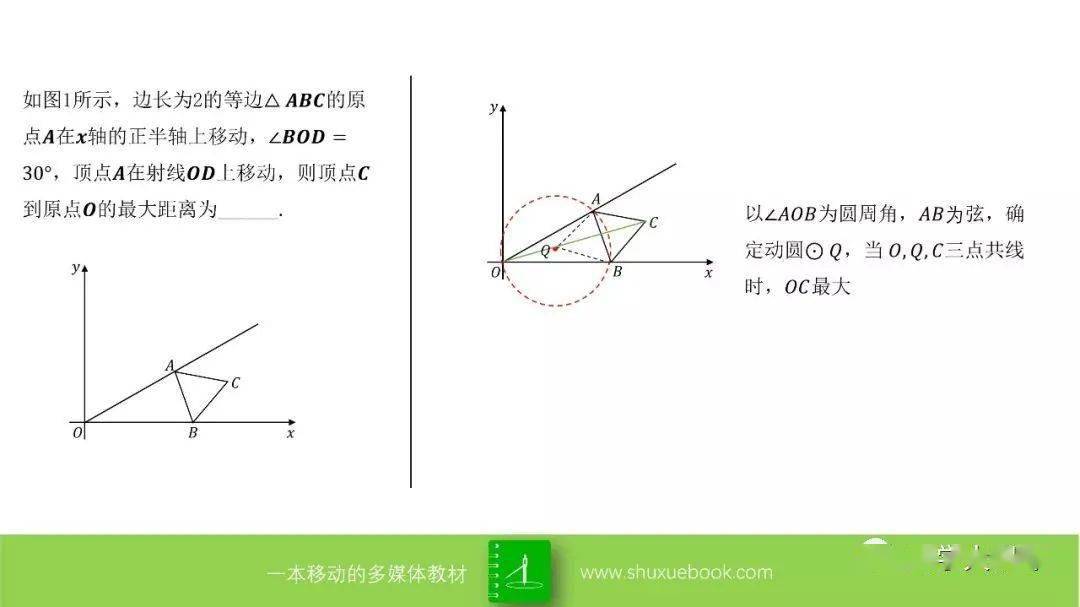

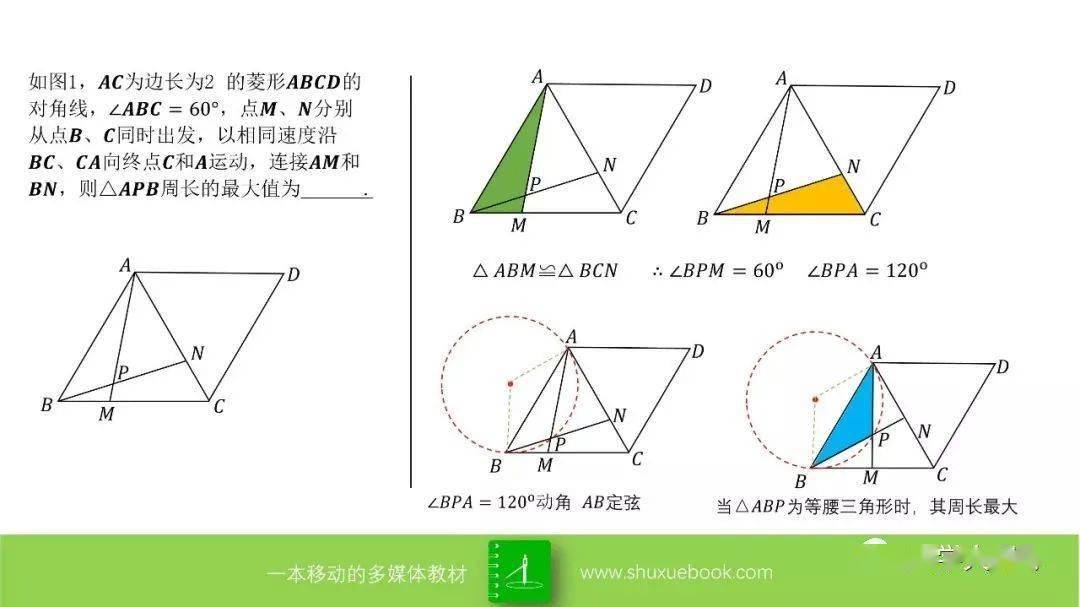
致亲爱的你:
Dear,因公众号后台进行改版,不在按时间先后顺序为大家推送文章,而是采用算法排列文章顺序——排序的标准,跟你阅读这个公众号的频率有很大的关系。时间算法的打乱很可能会让你与我擦肩而过。
所以恳请大家:在翻看公众号的时候,多留意一下一直陪在您身边的“三好网”,多看看三好网的文章。连续看一段时间,微信就知道了,你还挺中意“三好网”哒 ,以后三好网就会重新出现在靠前的位置跟大家见面啦 !拜托大家啦 !