考研数学三中的概率论与数理统计部分是许多考生需要重点攻克的难点。选择合适的参考书籍和老师对于备考至关重要。以下是一些备受好评的用书和老师：
1. 《森哥考研数学概率论与数理统计辅导讲义》：余丙森老师编写，适合基础薄弱的学生，内容细致，页面留白方便记笔记。
2. 《张宇考研数学》：张宇老师的书以系统性和逻辑性著称，适合需要强化逻辑理解的考生。
3. 《李永乐老师的考研数学复习全书》：李永乐老师的书籍通常注重基础与系统性，适合全面复习。
1. 王式安老师以深入浅出的教学风格和对命题的准确把握而闻名，课程重点突出，适合有一定基础的学生。
2. 张宇老师的课程系统性强，逻辑清晰，善于拆解复杂知识点，但节奏较快，适合自学能力较强的学生。
3. 余丙森老师在基础班中讲解细致，适合基础薄弱的学生，强化班可能需要额外辅导。
4. 方浩老师在数理统计方面有独到见解，适合需要深入理解统计学的考生。
5. 李良老师的课程注重基础，适合基础较差的学生，追求高分的学生可能需要额外强化。
当然每位老师都有自己的教学特点和优势，选择适合自己的老师非常关键。建议学生在正式选择之前，可以先试听几位老师的课程，找到最适合自己的教学风格和节奏。
最后，考研是一个长期而艰巨的过程，需要耐心和毅力。希望每位考生都能找到适合自己的学习方法，顺利通过考试。
接下来，噔噔蹬蹬！二战人来了！我将详细描述我在一战和二战中的经历以及一些经验，特别是我所遇到的问题和踩过的坑。希望这些经验能对大家有所帮助。
二战回顾考研在考数学的专业里，得数学则上岸！！！
考研是个漫长的过程，在这个过程中，除了有坚定的毅力以外，最重要的就是不要走太多弯路浪费时间。
在我第一次考研时，就是因为浪费了太多时间，虽然很累，但是自己的知识缺口仍然很大，才导致了最后的失败。
一战时我一直在找寻适合自己的学习方式，特别是数学这只拦路虎。
我看课一直在试不同的老师，拿起习题却发现自己无从下手便又开始无尽地看课，等我意识到必须要开始做题了的时候，已经完全来不及了。
我觉得我自己就是考研数学复习的大多数，一战结束时不得不接受考试现实真实而残酷。
我的问题主要在于我自己就是没有努力到点子上去，一战时虽然总结也写了，视频课也看了，题也刷了，但没有把努力转换成分数。
一战的教训一战失败后的反思中，我发现最大的问题在于自己动手解题能力不够强。
有句话说得好，你看到的不一定是你真正看到的。对于习题而言，就是这样的情况。你看到一道习题，如果你不会做，你可能会去查看答案，然后以为自己掌握了，但事实上你只是记住了答案而已，并没有真正掌握。
正是因为这一点，我要给所有同学的建议是一定要注重 "做题+练习计算能力" 这个重点。
然而，简单粗暴的题海战术不是提高数学成绩最有效的方法，应该有针对性地做题才能提高对知识点的掌握能力。
对于我的二战来说，我选择从题目入手重新学习和消化知识点。当时我使用了一个刷题平台，名叫「知能行考研数学」
知能行考研数学知能行考研数学通过大数据分析历年真题的考点难点，为每位考生选择快速提高的突破口。知能行基于机器学习追踪考生知识点的掌握情况，测练合一从而达到高效备考
https://bestzixue.com/?app_referrer_id=DXW~atczc-laOlyl-0629-editor_jnx
我二战全程使用了这个平台，因为知能行能够让我有针对性地做题，一层层的夯实基础，简单来说就是能够把知识点分解成小模块来消化，从而建立一个完整无死角的知识框架。
在进行数学学习和复习的过程中，平衡观看课程和做题练习是至关重要的。
我一战就是一味看视频，不进行做题输出，到了后期才去做题，才发现会出大问题 …
我发现光是看视频进行学习经常会发生一种情况，就是看完了整个视频，甚至也做了笔记，但是看完之后却说不出到底从中获得了什么知识。
但如果直接做题又会有一种两眼一抹黑的情况发生，这样非常不利于我们对于自己做题的主动性。
在使用知能行进行学习时，每一章开始前都会有一个「复习要点」，包括了核心的知识框架。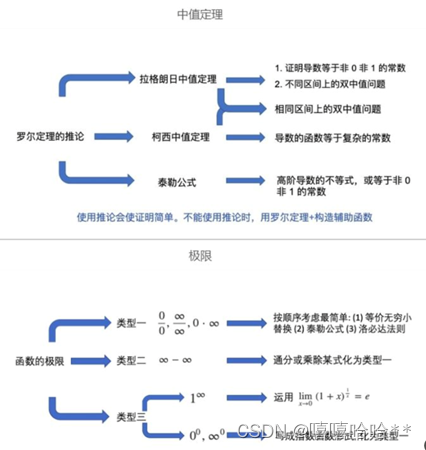
在听课时，经常会发生听完一节课，但“脑袋空空”的情况，这种情况下我们就可以在看视频前通过这个知识点列表来明确目标，从而更高效地看课。
特别应该利用好知能行的查拆分知识点的功能。先了解本章有哪些知识点，再带着对这些知识点的疑惑去看视频中老师是如何讲解，怎么样推出这样的结论的。
这样能让我们避免看完视频仍然脑袋空空的情况。
看完课就可以用知能行对这一章进行练习，做题练习是巩固知识、检验理解程度的有效方式。这在对之前看过的知识点起到加强作用的同时，也能查漏补缺。
像这样采取看视频和做题交替进行的方式。可以确保你在学习过程中既能够获取新知识，又能够及时巩固和应用所学内容。
缺乏目标的规划一开始每当我遇到不会的题，就去翻答案，去背答案。最后发现这只是“虚假”地学会了某道题，而不是学会了一类题，甚至这一题都不一定保证下次能做对。
而把一道题彻底弄明白底层逻辑，看似用了